3.Bellman Optimality Equation

Optimal Policy and Bellman Optimality Equation

本节内容

• 核心目标：最优 state value 与最优策略
• 基础工具：Bellman 最优方程

Motivating examples

回顾 state value 和 action value 的例子

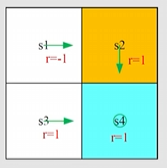
根据上述确定的策略、状态转移、奖励分布，由如下 Bellman 公式

$$\begin{array}{rl}{v}_{\pi }(s_1)& =-1+\gamma v_{\pi }(s_2),\\ v_{\pi }(s_2)& =1+\gamma v_{\pi }(s_4),\\ v_{\pi }(s_3)& =1+\gamma v_{\pi }(s_4),\\ v_{\pi }(s_4)& =1+\gamma v_{\pi }(s_4).\end{array}$$

取 $\gamma =0.9$ 则求解 Bellman 方程解如下：结果表示越靠近目标state value 越大

$$\begin{array}{rl}{v}_{\pi }(s_1)& =-1+\frac{\gamma }{1-\gamma }=\frac{0.9}{1-0.9}-1=8,\\ v_{\pi }(s_2)& =\frac{1}{1-\gamma }=\frac{1}{1-0.9}=10,\\ v_{\pi }(s_3)& =\frac{1}{1-\gamma }=\frac{1}{1-0.9}=10,\\ v_{\pi }(s_4)& =\frac{1}{1-\gamma }=\frac{1}{1-0.9}=10.\end{array}$$

得到每个状态下的state value 后计算action value

$$\begin{array}{rl}{q}_{\pi }(s_1,a_1)& =-1+\gamma v_{\pi }(s_1)=6.2\\ q_{\pi }(s_1,a_2)& =-1+\gamma v_{\pi }(s_2)=8\\ q_{\pi }(s_1,a_3)& =0+\gamma v_{\pi }(s_3)=9\\ q_{\pi }(s_1,a_4)& =-1+\gamma v_{\pi }(s_1)=6.2\\ q_{\pi }(s_1,a_5)& =0+\gamma v_{\pi }(s_1)=7.2\end{array}$$

发现问题：这个例子在 $s_1$ 时的策略 $\pi (a|s_1)$ 是不太好的，因为右走是禁止区域。应该如何优化策略？

$$\pi (a|s_1)=\{\begin{array}{ll}1& a=a_2\\ 0& a\ne a_2\end{array}$$

解决：假如选择最大的action value，那么就可以产生一个新的决策：

$${\pi }_{\text{new}}(a|s_1)=\{\begin{array}{ll}1& a=a^{\ast }\\ 0& a\ne a^{\ast }\end{array}$$

其中 $a^{\ast }=\arg {\max }_a{q}_{\pi }(s_1,a)=a_3.$

为什么这能够优化策略？

虽然action value 能够用来评估action 的好坏，但上述的优化是基于其他状态已经是最优策略的情况下进行的。如果其他状态下的策略是随机的或者不是最优的呢？数学上可以保证只要重复迭代，（每个状态都选择action value 最大的action，然后新的action 构成新策略，利用这个策略再迭代得到新策略）一定会得到最优策略

Definition of optimal policy

State value 能够衡量策略的好坏，因为Bellman 方程是对 action value 的平均，如果策略使得平均行动都价值高，则该策略是好的：$if{v}_{{\pi }_1}(s)\ge v_{{\pi }_2}(s)foralls\in \mathcal{S},then{\pi }_{1}isbetterthan{\pi }_2$

定义

一个决策 ${\pi }^{\ast }$ 是最优的，如果 $v_{{\pi }^{\ast }}(s)\ge v_{\pi }(s)foralls\in \mathcal{S}andforanyotherpolicy\pi$

提出定义后，就会自然产生问题：

• 最优策略存在？
• 最优策略唯一？
• 最优策略随机还是确定？
• 如何得到最优策略？

Bellman Optimality Equation

1.BOE:introduction

由策略好坏的定义，Bellman 方程中应该取使得 state value 最大的决策 $\pi$

Element form

$$v(s)=\underset{\pi }{\max }\sum _a\pi (a|s)\left(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v(s^{\prime })\right),\forall s\in S$$

Matrix form 以简洁的方式刻画了最优策略和最优 state value

$$\begin{array}{rl}v& =\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }v)\\ where[r_{\pi }{]}_s\triangleq \sum _a\pi (a|s)\sum _{r}p(r|s,a)r& ,[P_{\pi }{]}_{s,s^{\prime }}=p_{\pi }(s^{\prime }|s)\triangleq \sum _a\pi (a|s)p(s^{\prime }|s,a)\end{array}$$

问题：求解算法、存在性、唯一性、与最优策略有什么关系

2.BOE: Maximization on the right-hard side

BOE 存在未知量 $v$，存在需要最大化的策略 $\pi$，因此可看成一个式子两个未知量

$$v(s)=\underset{\pi }{\max }\sum _a\pi (a|s)\left(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v(s^{\prime })\right),\forall s\in S$$

example 1 (如何求解一个方程中的两个未知变量)

考虑有未知变量为 $x,a$ 的方程 $x={\max }_a(2x-1-a^2)$

• 先对右侧求解 ${\max }_a(2x-1-a^2)=2x-1$，此时 $a=0$
• 方程变为 $x=2x-1$，进而求解的 $x=1$
• 因此方程解为 $a=0,x=1$

可以先给定一个初值 $v(s^{\prime })$，则公式可化简，因此可有上述顺序求解方程，（后面又数学证明保证迭代收敛性）

$$\begin{array}{rl}v(s)& =\underset{\pi }{\max }\sum _a\pi (a|s)\left(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v(s^{\prime })\right),\forall s\in S\\ & =\underset{\pi }{\max }\sum _a\pi (a|s)q(s,a)\\ & =\underset{\pi }{\max }[\pi (a_1|s)q(s,a_1)+,...,+\pi (a_n|s)q(s,a_n)]\end{array}$$

example 2 (如何求解 ${\max }_{\pi }{\sum }_a\pi (a|s)q(s,a)$)

考虑给定 $q_1,q_2,q_3$ 的情况下求解 $ma{x}_{c_1,c_2,c_3}{c}_1{q}_1+c_2{q}_2+c_3{q}_3$，其中 $c_1+c_2+c_3=1$, 且 $c_1,c_2,c_3>0$，假设 $q_3>q_1,q_2$

• 因为 $c_1{q}_1+c_2{q}_2+c_3{q}_3\le (c_1+c_2+c_3)q_3=q_3$
• 则最优解为 $c_3^{\ast }=1,c_1^{\ast }=c_2^{\ast }=0$

由 example 2 可知

$$\underset{\pi }{\max }\sum _a\pi (a|s)q(s,a)=\underset{a\in \mathcal{A}(s)}{\max }q(s,a)$$

则最优策略为

$$\pi (a|s)=\{\begin{array}{ll}1& a=a^{\ast }\\ 0& a\ne a^{\ast }\end{array},where{a}^{\ast }=\arg \underset{a}{\max }q(s,a)$$

3.BOE: Rewrite as $v=f(v)$

由于 BOE 方程时 $v$ 的函数，可以写成下式矩阵形式。

$$v=\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }v):=f(v)$$

其中 $f(v)$ 的元素为：

$$[f(v){]}_s=\underset{\pi }{\max }\sum _a\pi (a|s)q(s,a)$$

4.Contraction mapping theorem

相关概念

不动点：若 $f(x)=x$，则称 $x\in X$ 是 $f:X\to X$ 的不动点

压缩映射：若 $||f(x_1)-f(x_2)||\le \gamma ||x_1-x_2||$，$\gamma \in (0,1)$ 则称 $f$ 是一个压缩映射

• $\gamma$ 必须严格小于 1，因此 ${\gamma }^k\to 0$ 被 $k\to 0$ 控制
• $||.||$ 为向量范数

相关概念的相关例子

$x=f(x)=0.5x$ 易得：

• $x=0$ 为 $f$ 的不动点
• $||0.5x_1-0.5x_2||=0.5||x_1-x_2||\le \gamma ||x_1-x_2||,\gamma \in [0.5,1)$，故$f$ 为压缩映射

$x=f(x)=Ax$ 矩阵形式时, $||A||\le \gamma <1$

• $x=0$ 仍然是不动点
• $||A{x}_1-A{x}_2||\le ||A||.||x_1-x_2||\le \gamma ||x_1-x_2||$，$f$ 为压缩映射，这倒没推导过

压缩映射定理：

如果 $f=f(x)$ 是压缩映射，则存在唯一不动点，且可通过点序列 $\{x_k\}$ 递归迭式 $x_{k+1}=f(x_k)$ 满足 $x_k\to x^{\ast }(x_k\to \infty )$

5.BOE:solution

回过来看 Bellman 方程：$v=f(v)={\max }_{\pi }(r_{\pi }+\gamma P_{\pi }v)$

可以证明 $f(v)$ 是一个压缩映射！则可以使用压缩映射定理exist unique 的不动点 $v^{\ast }$ ，且可通过序列 $\{v_k\}$ 和迭代式 $v_{k+1}=f(v_k)={\max }_{\pi }(r_{\pi }+\gamma P_{\pi }{v}_k)$ 进行求解，给定任意初值 $v_0$ 序列 $\{v_k\}$ 会快速收敛到 $v^{\ast }$，收敛速度取决于 $\gamma$

假设 $v^{\ast }$ 是 Bellman 方程的解，则 $v^{\ast }={\max }_{\pi }(r_{\pi }+\gamma P_{\pi }{v}^{\ast })$

此时的最优策略为 ${\pi }^{\ast }=\arg {\max }_{\pi }(r_{\pi }+\gamma P_{\pi }{v}^{\ast })$

因此得到 Bellman 最优方程(BOE)$v^{\ast }=r_{{\pi }^{\ast }}+\gamma P_{\pi }{v}^{\ast }$

• BOE 是特殊的 Bellman 方程
• ${\pi }^{\ast }$ 是最优策略（为什么？）
• 其中 $v^{\ast }$ 是最优策略对应的state value（state value 是所有决策中最大的吗？）

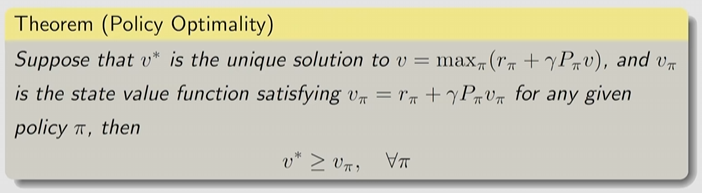
6.BOE:optimality

最优策略具体是怎样？实际上在第 2 节中的求解例子已知

Analyzing optimal policies

最优策略的影响因素有哪些？如下 BOE

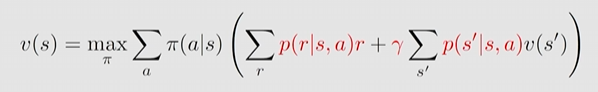
策略 $\pi (a|s)$ 与 $v(s),v(s^{\prime })$ 的计算结果由红色部分影响：

• 奖励设计：$r$
• 系统模型：$p(r|s,a),p(s^{\prime }|s,a)$
• 折扣率：$\gamma$

example 1 参数 $\gamma$ 的影响

由下图可知(a) 的最优策略是会进入forbiden区域的，但是如果设置更小的 $\gamma$，则(b)会避免进入forbidon 区域。

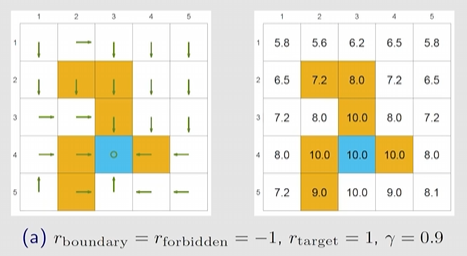
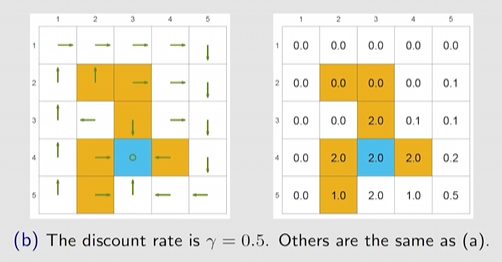
原因：

考虑 trajectory：$S_t\stackrel{A_t}{\to }{R}_{t+1},S_{t+1}\stackrel{A_{t+1}}{\to }{R}_{t+2},S_{t+2}\stackrel{A_{t+2}}{\to }{R}_{t+3},...$

其 return 计算： $G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...$

求 return 的期望，即状态价值： $v_{\pi }=\mathbb{E}(G_t|S_t=s)$

• 显然 $\gamma$ 越大，则越近视，
• $\gamma$ 越小，只看相对大小，相对来说是远处的奖励权重相对的便重要了！
• 极端的若 $\gamma =0$ 如下图，只关注瞬时奖励，极其短视

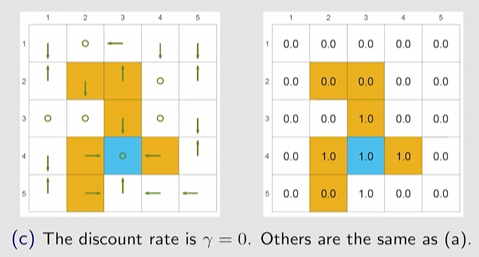
Example 2 参数 $r$ 的影响

显然瞬时惩罚变得更重后，绕路的 return 会大于走捷径的 return，因此会绕路

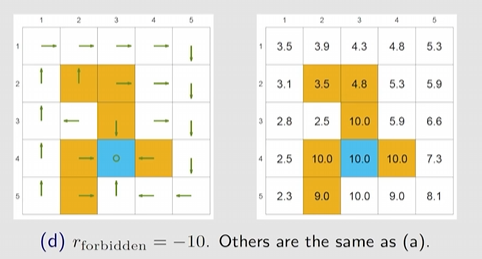
若对奖励做线性变换 $r\to ar+b$ 后如何？答案是不会改变，因为策略选择过程中是看相对好坏。数学证明如下，具体在书中：

Example 3 绕路

下图说明绕路的策略会使得 $v$ 更小，即绕路更差、

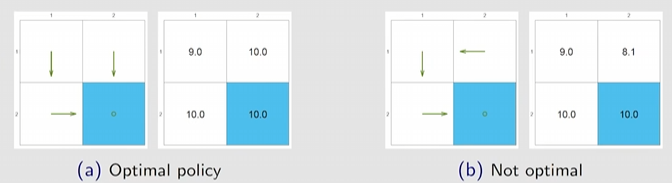
可能的提问，从 $(0,1)$ 出发，既然白色区域没有惩罚，为什么绕路会更差？因为：

Policy 1: $return=1+\gamma 1+{\gamma }^{2}1+{\gamma }^{2}1+....=10$

Policy 2: $return=0+\gamma 0+{\gamma }^{2}1+{\gamma }^{2}1+....=8.1$

Summary

• Bellman 最优方程的 elementwise form：
  • $v(s)={\max }_{\pi }{\sum }_a\pi (a|s)\left({\sum }_{r}p(r|s,a)r+\gamma {\sum }_{s^{\prime }}p(s^{\prime }|s,a)v(s^{\prime })\right),\forall s\in S$
• Bellman 最有方程的 matrix form：
  • $v={\max }_{\pi }(r_{\pi }+\gamma P_{\pi }v)$
• 通过压缩映射定理，BOE 存在唯一的解（策略不一定唯一）
• 通过压缩映射定理，可用迭代算法收敛到最优策略和最优的解
• BOE 的意义：因为因为该解的 state value 和 policy 都是最优的