2024 Survey of CAT

文献笔记

2024 Survey of Computerized Adaptive Testing A Machine Learning Perspective

摘要

• CAT 是根据考生表现动态调整试题，为评估考生的熟练程度提供一种定制的方法
• 研究 CAT 中的认知诊断模型、题库构建、问题选择、测试控制，探索优化 4 个组件；通过当前方法优势、限制和挑战分析，开发出稳健、公平、高效的 CAT 系统
• 以机器学习视角，以 CAT 的核心问题“测试问题选择算法”进行研究

1. 引言

• CAT 简介
  • CAT 与一刀切的传统考试不同，是由于其根据每个考生的熟练程度提供题目，最大限度提高评估的准确性，缩短考试时间。
  • 本质上 CAT 在回答一个准确性和效率的问题：通过提供最少的问题，准确评估考生的真正熟练程度。
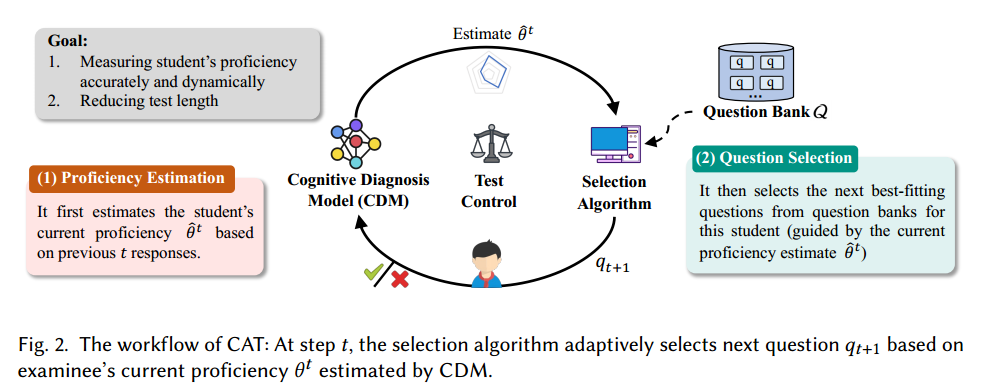
• CAT 系统包括四个轮流进行的主要组件：
  • 认知诊断：根据考生之前的回答估计当前熟练程度
  • 选择算法：根据一定标准从题库中选择下个问题
    • 传统标准是统计信息度量，如难度和考生熟练程度相符的问题，大约 50%可能答对。
  • 题库构建：需要大量题库，适应不同熟练程度的考生，实时决策。
  • 测试控制 (test control)：测试过程内容平衡性、公平性稳健性，CAT 结束后最终熟练度估计或者诊断报告结果
• CAT 代表机器智能和评估技术的融合：多决策问题需要复杂解决方案
  • 可靠性、公平性、搜索效率问题、管理题库、实时决策
• 机器学习中的 CAT：
  • 在机器学习角度，CAT 是关注数据效率的参数估计问题
  • 机器学习目标：从未标记的题库中选择最少数量的样本，在观察到它们的标签 (正确/错误的回答) 之后准确估计模型的潜在参数 (考生真实熟练程度)
  • 机器学习技术研究 CAT 中的四个主要组件：
    • 深度学习可诊断考生熟练程度，如 neural CD，KT 等
    • 自动构建题库
    • 数据驱动通过学习大规模响应数据优化选择算法
    • 机器学习关注诸如鲁棒性、搜索效率等因素提高 CAT 可靠性
• 本文贡献
  • 主要关注介绍选择算法的发展（因为这是 CAT 的核心组成部分）
  • 通过机器学习视角全面回顾 CAT 方案
  • 探索认知诊断、选择算法、题库构建、测试控制现有工作，并提供一个统一框架
  • 总结现有工作、讨论可靠 CAT 的关键因素
  • 开源模型和相关资源

2. CAT 背景

• CAT 发展
  • 1905 年作为智力测试开发适应性测试，1950 s 计算机将适应性测试转变为 CAT
  • 1970 s-1980 s 开创性整合了 IRT ，将问题难度和考生熟练程度相匹配，提高准确性，奠定 CAT 基础
  • 1990 s 贝叶斯、极大似然、最大信息方法等各种统计方法的应用于，GRE 托福等使用。
  • 机器学习通过大型数据集复杂分析、详细的行为建模，彻底改变 CAT。因为深度学习、自然语言处理、强化学习在问题表征、评分过程、自适应建模方面潜力巨大
• CAT 应用
  • 教育
    • 1980 s 护理执照考试、研究生考试 (GRE, GMAT) 和数学课程等
    • 较新的 CAT 变体：多阶段测试 (MST)，每个阶段一组问题；用于 GRE、法学考试、会计考试
  • 医疗保健
    • 心理健康评估（包括抑郁、焦虑、自杀风险量表等）
  • 社会学
    • 民意调查（降低成本）
  • 运动
    • 足球领域：衡量球员战术熟练程度，监控评估战术技能进展

3. 综述

• 明确问题：首先 CAT 假定考生的真实熟练程度 $\theta$ 是恒定的，那么 CAT 最终目标有两个
  • 使用回答估计考生的熟练程度，使其在考试结束时接近真实水平
  • 为每位考生选择最优价值和最合适的问题，缩短考试时间

3.1 任务形式化 ：

简单描述

• 首先，测试第 $t$ 道题目， $t\in [1,2,...,T]$，使用前 $t$ 个回答估计估计考生当前的熟练程度 ${\hat{\theta }}^t$
• 然后，利用当前熟练程度 ${\hat{\theta }}^t$ 在题库 $Q$ 中检索下一道题目 $q_{t+1}$ 给考生作答，作答结果为 $y_{t+1}$
• 由此相互作用形成相应序列 $\{(q_1,y_1),(q_2,y_2),...,(q_T,y_T)\}$，其中对题目 $q_t$ 作答正确记为 $y_t=1$ 否则为 0

严格形式化

为了达到 CAT 的两个目标，在每个测试中都需要以下两个步骤

• Step 1. 能力评估
  • 认知诊断模型预测具有熟练度的考生正确回答的概率，表示为 $f(q,\theta )=P(y=1|q,\theta )$，
  • 参数估计方法可用 MLE，Beyas 估计
  • 应用中损失函数经常使用二元交叉熵：给定前 $t$ 题的相应序列 $X_{1:t}=\{(q_1,y_1),(q_2,y_2),...,(q_t,y_t)\}$，则经验损失为 $L(\theta )={\Sigma }_{(q,y)\in X_{1:t}}l(y,f(q,\theta ))=-\Sigma [y\log f(q,\theta )+(1-y)\log (1-f(q,\theta ))]$
  • 因此优化损失函数 $L(\theta )$ 得到当前熟练度 ${\hat{\theta }}^t$ 估计：${\hat{\theta }}^t=\arg {\min }_{\theta }L(\theta )$
• Step 2. 选择问题
  • CAT 的核心是选择算法：利用考生当前水平 ${\hat{\theta }}^t$ ，从题库 $Q$ 中选择下一道题目 $q_{t+1}$,

$$q_{t+1}=\arg \underset{q\in Q}{\max }{V}_q({\hat{\theta }}^t)$$

其中 $V_q({\hat{\theta }}^t)$ 是问题 $q$ 的价值函数，$V$ 可以是一个测量题目能提供多少考生熟练程度的信息，或者它可能是设计成决定问题选择的策略分布 $\pi$ 输出

• 根据题目 $q_{t+1}$ 的新作答 $y_{t+1}$，使用 CDM 重新估计得 ${\hat{\theta }}^{t+1}$，这样的操作重复 $T$ 次，确保最后一步 ${\hat{\theta }}^T$ 估计接近真实的 ${\theta }_0$，因此给出 CAT 的定义
• 定义 1：CAT 定义
  • CAT 目标是找到一个大小为 $T$ 的问题集 $S=\{q_1,q_2,...,q_T\}$ ，使得由 $S$ 及其对应作答标签的最后一步估计 ${\hat{\theta }}^T$ 非常接近考生真实能力 ${\theta }_0$

$$\underset{|S|=T}{\min }||{\hat{\theta }}^T-{\theta }_0||$$

总结：直接优化 ${\theta }_0$ 是不实际的，因为这不可观测，甚至考生自己都不知道自己的熟练程度，因此现有的方法都是这个目标的近似值。

• 例 1：传统统计选择方法：利用 MLE 渐进统计特性减少不确定性
• 例 2：选择与考生当前估计的熟练程度匹配的问题
• 例 3：最近的子集选择方法试图确定 ${\theta }_0$ 的理论近似值作为优化新目标。

评估方法：为了验证估计的熟练程度，主要采用两种方法：

• 方法 1：使用 CDM 内考生估计值预测？没读懂
• 方法 2：模拟生成真实水平 ${\theta }_0$，模拟考生对每道题的回答，然后计算估计与模拟真值之间的均方误差。

3.2 分类

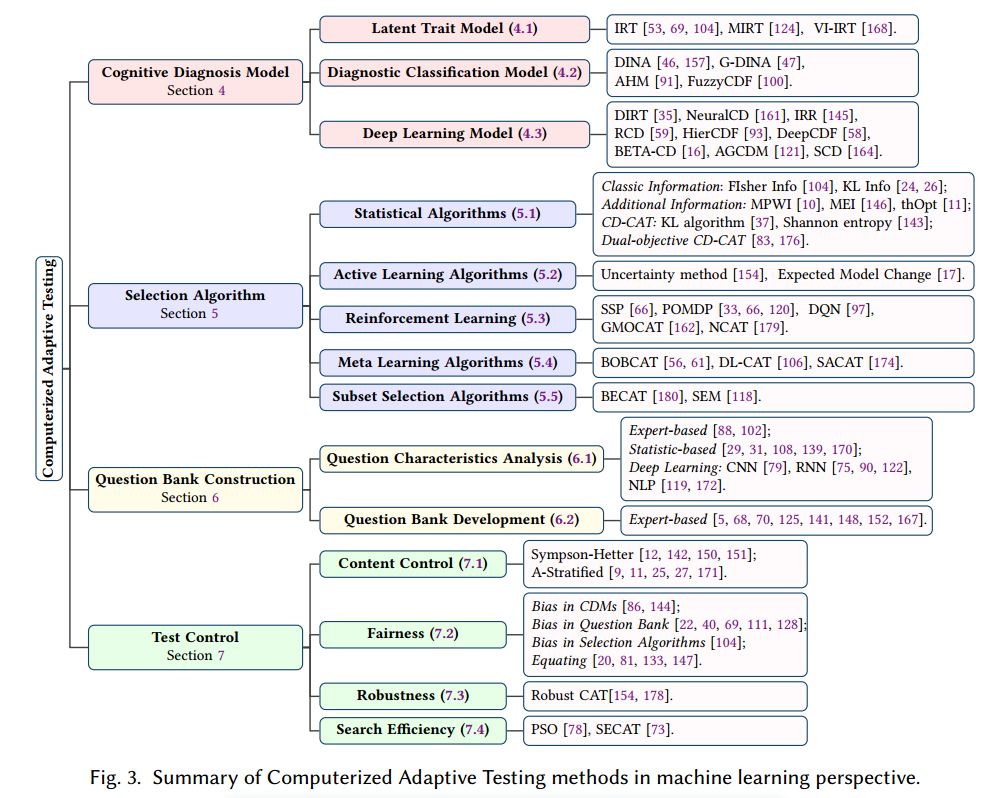
4. 认知诊断模型

现有 CDM 方法主要有三种类型，潜在特征模型、诊断分类模型、深度学习模型；分类标准是熟练程度表征的性质

1. 整体的数值能力值（潜在特征模型）
2. 跨越不同知识概念的离散认知状态（诊断分类模型）
3. 深度学习统一建模（深度学习模型）

4.1 潜在特征模型

模型例子：

• 潜在特征模型的代表：项目反应理论中 IRT 中，熟练程度是一个综合能力，表示为 $\theta$，可用三参数 $({\beta }_j,{\alpha }_j,c_j)$ Logistic 模型建立交互函数，来模拟考生正确回答问题 $j$ 的概率。

$$f(q_j,\theta )=c_j+\frac{1-c_j}{1+e^{-{\alpha }_j(\theta -{\beta }_j)}}$$

参数解释：

• 难度系数 ${\beta }_j$ 是对应了回答问题正确率为 50%的熟练程度（对应熟练程度，对应曲线的中点）
• 判别参数 ${\alpha }_j$ 表示对不同能力学生的区分度，因为越大曲线越倾斜，越倾斜表示越被试者被快速分成两类熟练程度，即区分效果越好（对应无量纲的系数）
• 猜测参数 $c_j$ 表示熟练程度低的考生还是能整正确做对题目的概率（对应概率）

IRT 模型现状、优缺点

• 上述参数都是预先计算好的，如今的 SAT、GRE 测试都是使用 IRT 开发，具有不错的测量可靠性和解释性
• IRT 模型还能够扩展成多维，对多个潜在特征进行建模。
• 但是他的性能受到简单交互函数的限制，缺乏考生对单个知识概念的细粒度建模。

4.2 诊断分类模型 (DCM)

诊断分类模型是 CMDs 的典型代表，考生的熟练程度对单个知识概念而言，通常为掌握与否的二分类。

模型例子：

• DINA 方法中考生的熟练程度为 $\theta =\{{\theta }_{(}1),{\theta }_{(}2),...,{\theta }_{(}K)\}$，对 $K$ 个知识概念的掌握与否二分类
• 如果给定二元 $Q$ 矩阵，$Q{\in }^{|Q|\times K}$，表示题目与知识概念的考察情况。
• 因此考生对题目 $j$ 的二元反应变量为 ${\prod }_{k,Q_{jk=1}}{\theta }_{(k)}$，则考生正确回答问题 j 的概率为：

$$f(q_j,\theta )=(1-s_j{)}^{{\prod }_{k,Q_{jk=1}}{\theta }_{(k)}}{g}_j^{1-{\prod }_{k,Q_{jk=1}}{\theta }_{(k)}}$$

参数解释：

• $s_j$ 是失误系数，尽管熟练掌握也可能做错
• $g_j$ 是猜测参数，尽管没掌握也可能猜对

DINA 模型现状

• 扩展的 G-DINA 提供考生熟练程度的细粒度视图？
• FuzzyCDF 使用模糊集理论从客观和主观数据中进行诊断
• 属性层次法 (AHM)，应用规则空间理论构建知识依赖，并将考生熟练程度与最接近的理想认知模式对齐，获得诊断结果
• 与潜在特征模型相比，诊断分类模型提供更细致全面的评估，并擅长多个知识概念个人的优缺点反馈，这对 CAT 干预非常重要

4.3 深度学习模型

深度学习方法适合大规模数据场景下的认知诊断，因为相比传统的模型，深度学习效率、考生和问题的复杂交互能力更强。模型例子：

• DIRT 用神经网络从问题文本中捕获语义信息
• NeuralCD 利用非负全连接神经网络捕捉复杂相互作用

4.4 讨论 1

讨论 1

• 由于 CAT 只能获得有限数量的考生回答来进行熟练程度估计，在某种程度上，CAT 被视为冷启动情境下的认知诊断。
• CDM 性能是确保 CAT 中熟练度估计准确性的关键因素
• 同时，CDM 选择会显著影响相应问题选择算法的选择

5. 选择算法

选择算法是 CAT 的核心

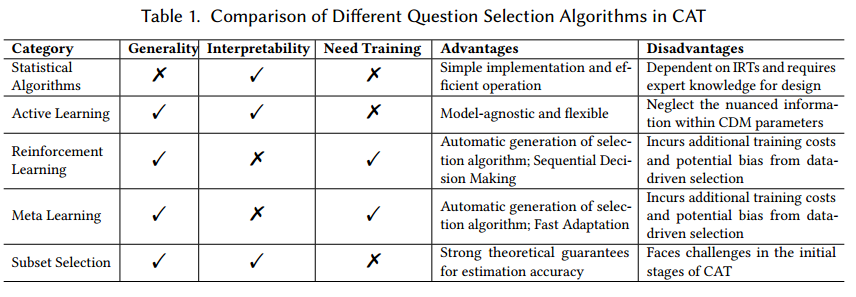
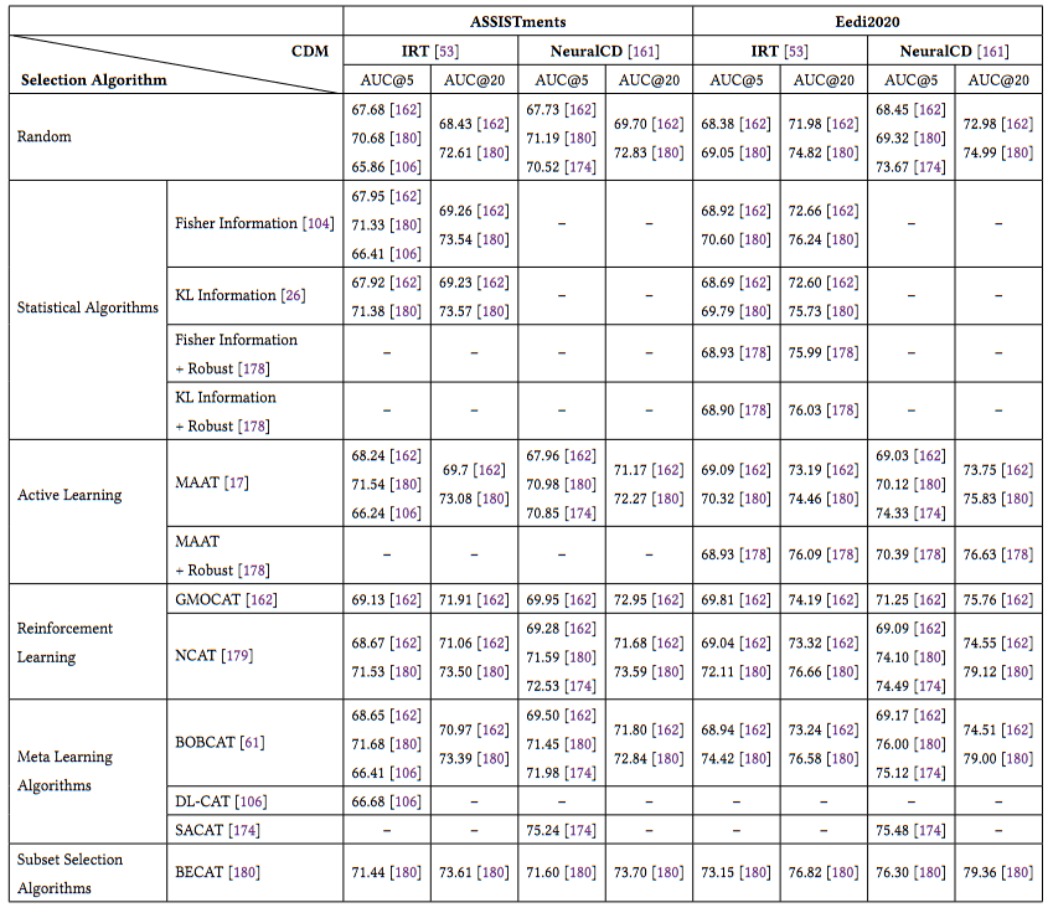
5.1 统计算法

本节建立统计问题选择的框架和方法，设计定义和确定信息度量，如 fisher 信息或者 kullback-Leibler 信息

1. CAT 中统计方法的一般流程

• 为题库 $Q$ 的每个问题分配一个价值数值
• 使用这个值分配方法作为启发式函数，在测试过程中不断选择最优价值的问题
• 从统计学的角度，这个问题选择策略是将问题价值定义为提供学生潜在能力的信息量

下一个问题索引 $j_{t+1}$ 基于当前估计 ${\hat{\theta }}^t$ 从题库 $Q$ 中选择：

$$j_{t+1}=\arg \underset{q_j\in Q}{\max }{I}_j({\hat{\theta }}^t)$$

其中 $I_j$ 是问题 $q_j$ 的信息量，由于 CAT 假设每个考生有一个真实的熟练程度 ${\theta }_0$，则可将其视为参数估计过程。因此问题的信息量可以解释为该问题的回答对参数估计的预期贡献。

2. Fisher 信息量

定义： $Fisher$ 信息是测量可观测随机变量 $X$ 携带的未知参数 $\theta$ 的信息量方法，其中 $X$ 的概率依赖于参数 $\theta$。(测量可观测随机变量携带的关于位置参数的信息量，该位置参数的概率依赖于随机变量。)

$Fisher$ 信息量公式：

$$n样本Fisher信息量:I(\theta )=E_x[({\nabla }_{\theta }L(X|\theta {)}^2)]=-E_x[{\nabla }_{\theta }^{2}L(X|\theta )]$$ $$似然函数：L(X|\theta )=\ln l(X|\theta )=\ln \prod _{i=1}^{n}f(x_i;\theta )$$

$Fisher$ 信息量应用于 CAT 背景：

• 假设每个学生都有一个真实的熟练度 ${\theta }_0$，$\theta$ 决定对题目 $q_j$ 的回答正确与否 $y_j$，随机变量写作 $X_j=(q_j,y_j)$
• 以 $3PL-IRT$ 为例，其中回答正确与否的概率密度函数为

$$f(q_j,\theta )=c_j+\frac{1-c_j}{1+e^{-{\alpha }_j(\theta -{\beta }_j)}}$$

• 由于回答正误是 01 变量，因此对第 $j$ 道题目的作答似然函数取交叉熵

$$L_j(Y|\theta )=y_j\ln f(q_j,y_j)+(1-y_j)\ln (1-f(q_j,y_j))$$

• 根据似然函数可计算每道题目的 $Fisher$ 信息量，即每道题目含有 ${\theta }_0$ 的信息大小

$$I_j(\theta )=E_{y_j}[({\nabla }_{\theta }{L}_j(Y|\theta ){)}^2]=\frac{({\nabla }_{\theta }f(q_j,\theta ){)}^2}{f(q_j,\theta )(1-f(q_j,\theta ))}=\frac{{\nabla }_{\theta }f}{f(1-f)}$$ $$其中似然函数一阶导\frac{\partial L_j(\theta )}{\partial \theta }=\frac{(y_j-f){\nabla }_{\theta f}}{f(1-f)}$$

• 带入密度函数 $f(q_j,\theta )$，但是 ${\theta }_0$ 是不可直接测的，因此需要利用学生部分作答估计当前熟练度 ${\hat{\theta }}^t$ (用诊断模型)

$$I_j({\hat{\theta }}^t)=\frac{(1-c_j){\alpha }_j^2{e}^{{\alpha }_j({\hat{\theta }}^t-{\beta }_j)}}{(1+e^{{\alpha }_j({\hat{\theta }}^t-{\beta }_j)}{)}^2(1-c_j+c_j(1+e^{{\alpha }_j({\hat{\theta }}^t-{\beta }_j)}))}$$

• 进而当前的 $Fisher$ 信息量 $I_j({\hat{\theta }}^t)$ 估计真实的 $Fisher$ 信息量 $I_j({\theta }_0)$

$Fihser$ 信息量一些结论

• 定理 1：最大似然估计的渐进分布，对于每一步 $t$，基于考生对前 $t$ 道题目的作答，当前熟练度极大似然估计满足渐近正态性

$${\hat{\theta }}^t\sim N({\theta }_0,\frac{1}{nI({\theta }_0)})$$

• 结论 1：随着题目和信息量增大，方差会减小；由于无偏估计，因此方差减小能够降低熟练度 ${\hat{\theta }}^t$ 估计不确定性。由于真实的熟练度 ${\theta }_0$ 未知，因此最大化 $Fisher$ 信息本质是降低估计方差，减少不确定性，增加估计效率
• 结论 2：但是如果估计 ${\hat{\theta }}^t$ 接近真值 ${\theta }_0$，那么最大化 $Fisher$ 信息 (MFI) 效果较好，但是如果差距很大，可能导致不准确
  • 优点：有理论基础、数学形式简单、计算效率高
  • 缺点：在测试初期，问题初始阶段由于问题数量太少，无法提供准确估计熟练度时，$Fisher$ 信息有效性没有理论上有效。

3. KL 信息

$KL$ 散度定义：在信息论中称为相对熵，度量两个概率分布之间的差异，$KL$ 散度越大说明差异越大

$KL$ 散度公式：

$KL$ 应用于 CAT 背景

假设学生真是熟练度为 ${\theta }_0$，对于任意 $\theta$，关于问题 $q_j$ 的 KL 信息测量了基于 ${\theta }_0$ 与 $\theta$ 的两个分布的差异，写作

$$K{L}_j(\theta ||{\theta }_0)=E_{y_j}\log [\frac{L(X_j|{\theta }_0)}{L(X_j|\theta )}]=f(q_j,{\theta }_0)\log [\frac{f(q_j,{\theta }_0)}{f(q_j,\theta )}]+(1-f(q_j,{\theta }_0))\log [\frac{1-f(q_j,{\theta }_0)}{1-f(q_j,\theta )}]$$

$K{L}_j(\theta ||{\theta }_0)$ 表示了两个熟练程度参数的区分程度，并不要求 $\theta$ 与 ${\theta }_0$ 接近。最大化 $KL$ 信息的问题选择相关算法

$$I_j({\hat{\theta }}^t)={\int }_{{\hat{\theta }}^t-\delta }^{{\hat{\theta }}^t+\delta }K{L}_j(\theta ||{\hat{\theta }}^t)d\theta$$

其中 $\delta =3/\sqrt{t}$，随着测试的序列长度增加，积分范围变小。

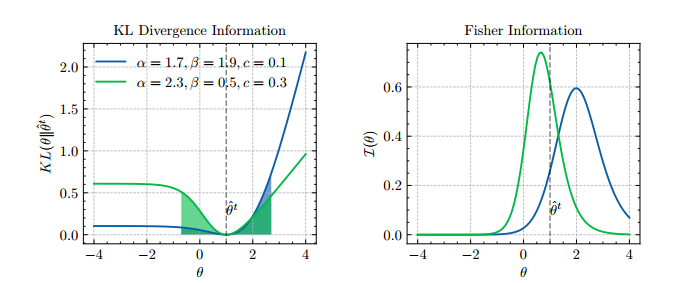
$KL$ 信息一些结论

• 结论 1：Fisher 信息的特定点的信息，而 KL 散度时基于全局信息度量
• 结论 2：本质上 $KL$ 方法确定的题目是能够提供考生可能的熟练程度的最大的差异
  • 解释：如下图，给定一道题目，x 轴为不同的 $\theta$ 取值，y 轴是给定 $\theta$ 与 ${\hat{\theta }}^t$ 的分布差异。
  • 由于 ${\hat{\theta }}^t$ 是对学生熟练度的估计，学生的熟练度也可能是 ${\hat{\theta }}^t+0.1$，${\hat{\theta }}^t+0.5$，${\hat{\theta }}^t+\delta$
  • 若 ${\hat{\theta }}^t+\delta$ 与 ${\hat{\theta }}^t$ 的差异越大，这个学生在以不同的熟练度去做这道题目实际上变化很大，因此越值得做。

4. 基于 Fisher 与 KL 的高级统计方法

相关工作：有大量基于 $Fisher$ 信息和 $KL$ 信息的工作，例如

• 极大似然加权信息选择策略
  • 通过考生当前回答的似然函数对 $Fisher$ 信息进行加权，原理与 $KL$ 信息相似，改变局部信息的局限性
  • 在第 $t$ 步时，最大化基于似然函数与 $Fisher$ 信息的加权

$$I_j({\hat{\theta }}^t)={\int }_{{\hat{\theta }}^t-\delta }^{{\hat{\theta }}^t+\delta }L(X_{1:t-1}|\theta )I_j(\theta )d\theta$$

• 后验加权信息选择策略
  • 公式如下，其中 $I_j(\theta )$ 可以时 fisher 或 KL 信息

$$I_j({\hat{\theta }}^t)={\int }_{{\hat{\theta }}^t-\delta }^{{\hat{\theta }}^t+\delta }P(\theta |X_{1:t-1})L(X_{1:t-1}|\theta )I_j(\theta )d\theta$$

• 最大期望信息策略
  • 加权 Fisher 信息时，考虑所有可能的结果，不仅是一个 $\delta$

得到信息量后，根据估计的熟练度和最大化信息量选择问题 $j_{t+1}=\arg {\max }_{q_j\in Q}{I}_j({\hat{\theta }}^t)$。因此这些方法目的时为了引入更多的信息，提高熟练度 $\theta$ 估计效率。

5. CD-CAT 中的选择算法

动机：

之前的选择算法都是基于 IRT 设计的，不适用于其他 cdm，例如 DINA 模型

认知诊断模型对学生表示熟练度的方法与 IRT 不同，其熟练程度表现为对一组离散知识点的掌握程度 (即认知状态)

基于认知诊断模型 CDM 的选择算法杯称为认知诊断 CAT (CD-CAT)

相关工作：

但是选择算法思想不变，最大化所选问题相关的特定信息，信息论的技术还是用到的，如 KL 散度，香农熵等。

• KL 算法目的是增强不同的潜在类别的区分
• 香农熵目的是减少考生潜在类别的不确定性

6. 统计算法的讨论 2

讨论 2

缺点：统计启发式方法需要领域专家考虑场景手动设计选择算法，例如 MFI 策略是以 IRT 设计，如果 CDM 方法改变，则选择策略需重新设计

5.2 主动学习算法

1. CAT 背景下的主动学习

动机：

• 理想的 CAT 应该与模型无关，即选择算法可使用不同的 CDM，因此需要通用的机器学习技术——主动学习 主动学习应用在 CAT ：
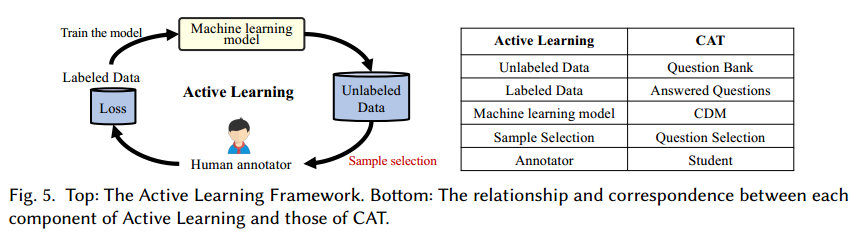
• 因为主动学习的目的与模式与 CAT 相似，如图，主动学习中，从一个机器学习模型和选择数据策略开始，每次对一个未标记数据进行标记后，提高模型性能。
  • 主动学习为标签数据：题库中的题目
  • 标签数据：问题的回答
  • 机器学习模型：CDM 模型（DINA、IRT 等）
  • 样本选择：问题选择
  • 标签者：学生（考生的答题行为是数据标注）
  • 选择尽量少的样本训练学习模型：选择尽量少的题目估计 CDM 中的熟练度参数

2. 主动学习的特点

关键的部分:

• CAT 的关键是问题选择策略，从主动学习的角度看是样本选择。现有方法一般从两个角度去选择：
  • 信息性：基于信息的选择算法，选择“能降低模型不确定性“的样本
  • 代表性：基于代表性的选择算法，选择“最能反映未标记数据的整体模式“的样本及其组合

为什么主动学习中的问题选择与模型无关

• 其核心思想是观测问题的回答后对熟练度估计的参数的改变

$$j_{t+1}=\arg \underset{q_j\in Q}{\max }{E}_{y_j}||{\nabla }_{\theta }L(X_{1:t}\bigcup \{(q_j,y_j)\}|\theta )||$$

• 计算每个结果梯度向量的期望范数，直觉上不管结果标签是什么，该框架偏向于对熟练度估计影响最大的题目。主动学习方法成功的解决模型依赖问题。

统计算法和主动学习算法的讨论：

3. 主动学习的讨论 3

讨论 3

• 缺点：包括统计算法和主动学习算法，这些属于启发式规则的方法，无法通过大规模考生响应数据学习来改进
• 泛化方法：数据驱动的方法克服该限制，且支持个性化测试。使用机器学习、深度学习方法有更好的性能，能在大规模考生回答中学习模式，自动选择合适的问题。
  • 强化学习
  • 元学习

5.3 强化学习算法 (RL)

1. CAT 中的强化学习

强化学习：

强化学习使智能体能够学习如何自动做出最佳决策。如自动驾驶、教育、医疗

根据行为奖励或惩罚进行反馈，目标是学习一个可以最大化的长期累计收益的策略

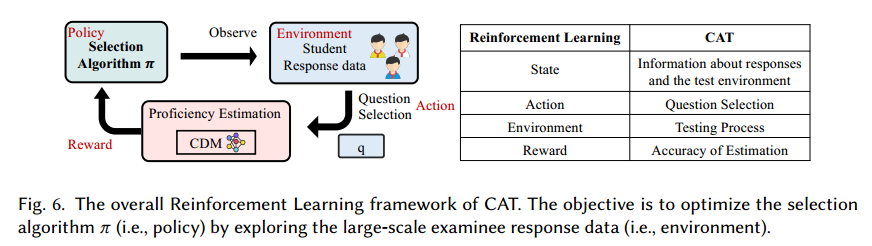
CAT 中的强化学习：

• 学生根据策略选择题目
• 根据选择的题目和 CDM更新学生状态
• 根据学生状态制定策略

2. 马尔可夫决策过程 (MDP)

马尔可夫决策过程：

相关概念参考强化学习笔记：

• 1.Basic concepts
• 2.Bellman Equation
• Set
  • 状态集 state：所有状态的集合 $S$
  • 行动集 action：所有行动的集合 $A(s)$ ，依赖于 $s$
  • 收益集合 reward：所有收益的集合 $R(s,a)$，依赖于 $s,a$
• 概率分布
  • 状态转移概率分布
    • $p(s^{\prime }|s,a)$，在当前状态 $s$ 和行动 $a$ 下，下一个状态 $s^{\prime }$ 的概率
  • 收益概率分布
    • $p(r|s,a)$ 在当前状态 $s$ 和行动 $a$ 下，收益为 $r$ 的概率
• 决策 policy
  • 在状态 $s$ 下，采取不同行动的概率 $\pi (a|s)$ 称为策略，这是行动的依据
• 马尔可夫性质：无记忆性，与历史无关
  • $p(s_{t+1}|a_{t+1},s_t,\dots ,a_1,s_0)=p(s_{t+1}|a_{t+1},s_t)$,
  • $p(r_{t+1}|a_{t+1},s_t,\dots ,a_1,s_0)=p(r_{t+1}|a_{t+1},s_t)$.
• 马尔可夫决策过程 markov decision process
  • Markov：无记忆性与历史无关
  • Decision：存在决策 policy
  • Process：状态根据行动到另一个状态
• 当 polily 给定后，即转移概率给定后，MDP 变为马尔可夫过程

2*. CAT 中的 MDP：

强化学习是探索环境，从行为中学习策略。应用于 CAT：探索能否从数据和学生互动中学习问题选择策略

状态：

$s_t\in S$ 表示测试步骤当前条件或情况，通常包括所有已回答的题目、当前熟练程度估计的潜在向量、题库候选题目：$s_t=(\{q_q,y_1,...,q_t,y_t\},Q)$

行动：

在当前状态下可从题库中选择的下一个问题 $A(s)=q_{t+1}\in Q$

奖励：

奖励 $r$ 是学生每次选择一个问题后受到的反馈。为了实现 CAT 目标，可定义为每个步骤的能力估计精度 $||{\hat{\theta }}^t-{\theta }_0||$。或者 $t$ 时刻在响应数据上的性能预测损失。

该奖励能指导策略选择，使得最优拟合问题中能减少估计误差

状态转移：

$p(s_{t+1}|s_t,q_{t+1})$ 表示在当前熟练程度 $s_t$ 下，做了下一道题目 $q_{t+1}$，能达到熟练程度 $s_{t+1}$ 的概率，并且对题目 $q_{t+1}$ 的作答正确与错误，转移概率分布也不一样。

2**. CAT 中 MDP 的相关工作：

利用 deep reinforcement learning DRL 来解决 MDP 问题，例如

• Li 用 Deep Q-Network (DQN) 表示行动价值函数 $Q_w(s,q)$，即 $s$ 状态，$q$ 问题下，用权重 $w$ 的全连接神经网络表示表示 $Q_w(s,q)$。其中可以根据最优化策略 $Q_w(s,q)$ 选择合适的题目 ${\pi }^{\ast }(q|s)=\arg \underset{q\in Q}{\max }{Q}_w(s,q)$
• 模拟考生和实体之间的复杂作用，zhuang 设计了基于 transformer 的 Q-Network，识别考生中的扰动 (guess 和 slip)

3. 随机最短路径公式 (SSP)

CAT 可定义为随机最短路径问题 (SSP)，这是 MDP 的特例

• SSP 目标是什么？：从初始状态 $s_0$ 到目标状态 $s_T$ 的最短路径。
• 目标状态是什么？：在 CAT 中，目标状态通常表示考试完成，或者达到设定的熟练度估计精度水平。

求解随机最短路径相关工作（没看懂）

• 用线性规划寻找最优测试策略，将问题视为流动网络，除了起点和终点每个状态必须具有平衡的流入和流出。
  • $x_{s,q}$ 表示预计每一对 $(s,q)$ 发生的频率，每个 $s$ 的相等的 $in(s)$ 和 $out(s)$ 流动模型
  • $in(s)$ 表示转移到 $s$ 的期望频率，转移到 $s$ 状态的其他所有状态 $s^{\prime }$ 下，所有行动的期望频率：$in(s)={\Sigma }_{s^{\prime },q}^{.}{x}_{s^{\prime },q}P(s|s^{\prime },q)$
  • $out(s)={\Sigma }_q{x}_{s,q}$
  • 目标函数：最大化总期望收益 $r$ ，即所有 $(s,q)$ 的期望频率乘以 $(s,q)$ 的收益 $r(s,q)$ 之和：

$$\underset{x_{s,q}}{\min }{\Sigma }_{s\in S,q\in Q}{x}_{s,q}r(s,q)$$

- 其中策略如何估计？因此最优化策略 $\pi^*$ 表示为：

$${\pi }^{\ast }(q|s)=\frac{x_{s,q}}{{\Sigma }_{q^{\prime }\in Q}{x}_{s,q^{\prime }}}$$

4. 部分可观测的 MDP (POMDP)

Agent 不能完全观察环境，MDP 是假设考生的熟练度能够从以前的回答中推断估计，其中熟练度可以是状态

但是一般情形下，熟练度不能够从以前的回答中完美推断估计：

• 作答中的干扰：考试过程受到学生行为和环境的不同的干扰，例如 guess 或者 slip
• 信息限制：测试只有有限的抽样问题，仅考察部分知识，不能完全反应综合能力
• 熟练程度的复杂性：熟练程度的定义可以是理解、分析、应用等知识概念，因此有限问题难以完整反映

将 CAT 建模成 POMDP ，相比 MDP ，POMDP 有两个元素

• $O$：一组观察结果
• $Z$：观察概率
• $Z(o|s^{\prime },q)$ 是在选择问题 $q$ 并且转移到状态 $s^{\prime }$ 后观察到 $o$ 的概率
• 状态仍然可以代表学生的熟练程度，但是现在状态不能被完全观察到。
• 所以状态存在一个概率分布 $b(s)$，成为信念状态，即 $s$ 表示根据作答记录，考生可能的熟练程度
• 同样用贝叶斯更新，当智能体在信念状态 $b$ 下，选择问题 $q$ 并观察到 $o$，更新信念状态

$$b^{\prime }(s^{\prime })=\eta Z(o|s^{\prime },q){\Sigma }_{s\in S}P(s^{\prime }|s,q)b(s)$$

• POMDP 有许多算法求解，例如网格搜索、蒙特卡洛等

5.4 meta 学习算法

1. CAT 背景下的 Meta：

Meta 学习算法：

基础学习者在各种任务中训练，收集见解和如何有效学习的一般知识，利用这些知识适应新的任务

Meta 用于 CAT 中：

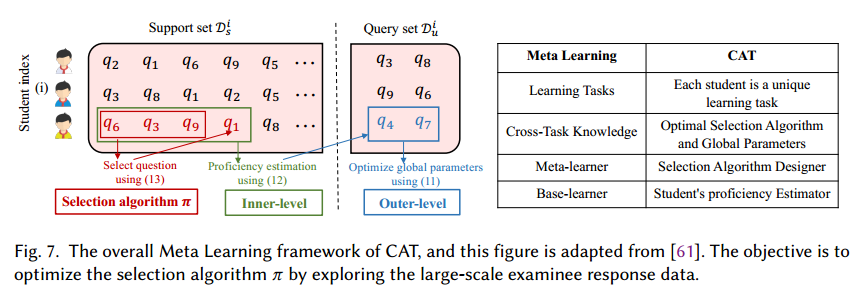
• 考生的考试过程被看作一项任务，任务涉及根据自己的熟练程度选择合适题目
• 选择算法可以被看作一项普遍知识，代表不同的考生群体中累计的知识和经验，例如最佳策略，考题信息，考生熟练度

2. Meta 的相关工作：

• Bi-Level Optimization 双层优化
  • Ghosh 提出 BOBCAT 双层优化框架，学习数据驱动选择算法 $\pi$。$N$ 为考生数量，每个考生 $i$ 的回答随机分为支持集 ${\mathfrak{D}}_s^i$ 和查询集 ${\mathfrak{D}}_u^i$，根据选择算法 $\pi$ 从支持集 ${\mathfrak{D}}_s^i$ 中选择 $t$ 个问题 $\{q{,}_{.}..,q_t\}$，观测作答并预测他们在查询集 ${\mathfrak{D}}_u^i$ 的作答。将全局知识定义为两目标优化问题
    • 其中 $l(y,f(q,{\theta }_i))$ 是预测作答与真实作答的交叉熵。
    • 公式 (2) 中是利用策略 $\pi$ 在 ${\mathfrak{D}}_s^i$ 中选择，最小化交叉熵损失估计熟练度 $\theta$
    • 公式 (1) 是利用策略 $\pi$ 在 ${\mathfrak{D}}_u^i$ 中选择，最小化交叉熵学习“选择算法 $\pi$”和“全局参数 $\gamma$”
      • 全局参数：问题特征和考生优先能力?
    • 简单理解：参数 $\theta$ 和策略 $\pi$ 的来回估计相互更新。

${\min }_{\theta ,\gamma }\frac{1}{N}{\sum }_{i=1}^N{\sum }_{(q,y)\in D_u^i}l(y,f(q,{\hat{\theta }}_i)),$

$s.t.{\hat{\theta }}_i=argmin{\sum }_{(q,y)\in D_s^i}l(y,f(q,{\theta }_i)),$

$where{q}_{t+1}\sim \pi \left(q|q_1,y_i(1),...,q_t,y_i(t)\right)\in D_s^i.$

• 基于 Bi-Level Optimization 的改进
  • Ma 提出解耦学习 CAT (DL-CAT)。原始的 BOBCAT 是用内外耦合来优化参数，DL-CAT 设计真值构造策略和成对损失函数独立训练。
  • Feng 引入 BOBCAT 的约束，解决测试重叠和问题暴露问题
  • Yu 引入考生协同信息优化两目标问题，实现熟练度估计快速收敛
• 元学习与强化学习的比较
  • 元学习可以重新定义为一个强化学习问题。
  • Zhuang 将 CAT 中的元学习问题转化为强化学习问题，提出 NCAT。由于考试可能根据不同的停止规则在任何一步停止，故 NCAT 简化了元学习的原始目标（公式 1）
    • 将所有测试步骤相加最小化损失，然后双目标优化被转化成强化学习中最大化期望累计收益

$$\begin{gathered} \underset{\pi }{\min }\frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T\sum _{(q,y)\in D_u^i}l(y,f(q,{\hat{\theta }}_i^t))\stackrel{\Delta }{=}\underset{\pi }{\max }{E}_{i\sim \pi }\left[\sum _{t=1}^T-\sum _{(q,y)\in D_u^i}l(y,f(q,{\hat{\theta }}_i^t))\right] \\ =\underset{\pi }{\max }{E}_{i\sim \pi }\left[\sum _{t=1}^T-L({\hat{\theta }}_i^t;D_u^i)\right], \end{gathered}$$

其中$where{\hat{\theta }}_i=argmin{\sum }_{(q,y)\in D_s^i}l(y,f(q,{\theta }_i)),And{\mathfrak{D}}_s^{i(t)}=\{q_1,y_{i(1)},...,q_t,y_{i(t)}\}$

• Wang 设计了多目标的 RL 框架，可以分别提高预测精度、增加知识概念、减少问题曝光？

3. RL 和 Meta 的讨论 4

数据驱动的机器学习方法 讨论 4

好处：

• 能够从数据中学习优化问题选择策略，实现 CAT 目标 $mi{n}_{|S|=T}||{\hat{\theta }}^T-{\theta }_0||$
• 可以分析学习行为、表现反应和偏好，揭示潜在模式和相关性

缺点：

• 训练成本巨大
• 因为存在于数据集中的偏差，因此引入了潜在风险

5.5 子集选择算法

CAT 定义出发

重述 CAT 定义 1：CAT 目标是找到一个大小为 $T$ 的问题集 $S=\{q_1,q_2,...,q_T\}$ ，使得由 $S$ 及其对应作答标签的最后一步估计 ${\hat{\theta }}^T$ 非常接近考生真实能力 ${\theta }_0$

$$\underset{|S|=T}{\min }||{\hat{\theta }}^T-{\theta }_0||$$

其中 $where{\hat{\theta }}_i=\arg \min {\sum }_{(q,y)\in D_s^i}l(y,f(q,{\theta }_i))$ 是最终在 $t=T$ 时对所有作答结束后的熟练度估计，不要求每一步都是最优，要求最终最优。

子集选择算法相关工作

全局角度看，本质上是子集选择问题。从一个大集合 $Q$ 中选择子集 $S$，在特定约束下优化目标函数 $F(S)$

问题：以 ${\theta }_0$ 表示的考生的真实熟练程度是未知的，因此优化时不可直接优化

• Mujtaba 使用测量的标准误差 (SEM) 接近优化目标 (SEM 提供了考试中熟练度估计的置信度)
  • 思想：估计值趋于稳定，则接近真实估计
  • 其中，$I_i(\hat{\theta })$ 是在熟练度 $\hat{\theta }$ 下的考生做题目 $i$ 时的信息量，则目标函数为 $F(S)$。
  • 每一步使用多目标进化算法，最大化精度和最小化题目书得到 Pareto-optimal 集合

$$\underset{|S|=T}{\min }\Vert \widehat{{\theta }^T}-{\theta }_0\Vert \Rightarrow \underset{|S|=T}{\min }\sqrt{\frac{1}{{\sum }_{i\in S}{I}_i({\hat{\theta }}^T)}}=\underset{|S|=T}{\min }F(S)$$

• Zhuang 提出有界估计 CAT 框架 (BECAT) ^290308 。以数据汇总的方式重新定义求解选择问题。
  • 思想，利用整个题库的信息去估计学生的理论最佳掌握 ${\theta }^{\ast }$
  • 将接近 ${\theta }_0$ 的问题转化成接近 ${\theta }^{\ast }$
  • 只选取规模为 $T$ 的问题集作为最终的推荐结果

$$\underset{|S|=T}{\min }||{\hat{\theta }}^T-{\theta }_0||\Rightarrow \underset{|S|=T}{\min }||{\hat{\theta }}^T-{\theta }^{\ast }||\Rightarrow \underset{|S|=T}{\min }\underset{\theta \in \Theta }{\max }\Vert \sum _{(q,y)\in S}\gamma \nabla l(y,f(q,\theta ))-\sum _{(q,y)\in Q}\nabla l(y,f(q,\theta ))\Vert$$ $$\begin{gathered} \Rightarrow \underset{|S|=T}{\min }\underset{\theta \in \Theta }{\max }\sum _{j\in S}\underset{j^{\prime }\in S}{\min }||\nabla l_j(\theta )-\nabla l_{j^{\prime }}(\theta )|| \\ \Rightarrow \underset{|S|=T}{\max }\sum _{i\in Q}\underset{j\in S}{\max }w(i,j),\text{\hspace{1em}(*)} \end{gathered}$$

各种选择算法的比较

6. 题库构建

6.1 问题特征分析

6.2 题库发展

7. CAT测试控制

7.1 内容控制

7.2 公平性

7.3 稳定性

7.4 研究有效性

8. 评估

熟练度估计评估

模拟实验，在基于考生给定的熟练度分布中抽样学生，通过做题交互去估计这个”真实的”熟练度 ${\theta }_0$

考生分数预测

将考生做过的题目和得分作为训练、验证、测试

基于一个假设：估计的熟练度越好，他应该在验证集、测试集中的分数预测更准确。

8.1 数据集

• Educational Assessment Datasets
• Real-World Educational Data
  • ASSISTments
  • Junyi Dataset
  • EdNet Dataset
  • Eedi 2020 Dataset
• Simulated Datasets

9. 未来研究机会

• 多维的评估过程
• 多阶段测试
• 生成式 AI 用于 CAT
• CAT 中实现可解释的机器学习
• 用于 AI 系统评估的 CAT