1.Basic concepts

课程笔记

基本概念

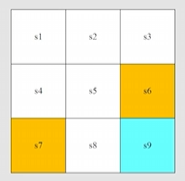
概念以如下图说明：

• 白色为可行位置
• 橙色为禁止位置 (能进入)
• 蓝色为目标位置
• 边界不可逾越

State

状态是智能体所处的环境状态，状态表示为 $s_i$，例如机器人所在的九宫格

State space

状态空间表示状态的集合，表示为 $S=\{s_i\}$，例如九宫格共有九个位置

Action

行动是第 $i$ 时刻采取的行为 $a_i$ ，例如机器人有上($a_1$)、右 ($a_2$)、下 ($a_3$)、左 ($a_4$)、不动 ($a_5$)五种行动

Action space of a state

行动空间是不同状态下的行动的集合，表示为 $A(s_i)=\{a_i\},s_i\in S$，显然行动的范围是与当前所处的状态相关。

State transition

状态转移：$s_1\stackrel{a_2}{⟶}{s}_2$ 定义了 agent 和环境的交互行为，例如机器人如果规定在状态 $s_1$ 必须右走，则转移概率 $p(s_2|s_1,a_2)=1$

Policy（unique）

策略是智能体在当前状态下应该做什么行动，用概率表示在最简单的情况下确定性情况下这么写

$\pi (a_1|s_1)=0$

$\pi (a_2|s_1)=1$

$\pi (a_3|s_1)=0$

$\pi (a_4|s_1)=0$

$\pi (a_5|s_1)=0$

$\Sigma \pi =1$

随机情况写可以这么写

$\pi (a_1|s_1)=0$

$\pi (a_2|s_1)=0.5$

$\pi (a_3|s_1)=0.5$

$\pi (a_4|s_1)=0$

$\pi (a_5|s_1)=0$

$\Sigma \pi =1$

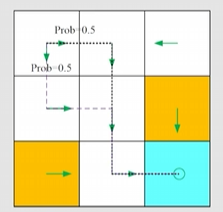
Reward

在采取行动之后得到一个奖励

• 正收益表示应该多采取这样的行动
• 负收益表示应该惩罚采取这样的行动

奖励的例子：

• 若行动出边界，奖励 $r_{round}=-1$
• 若行动进入禁止区域，奖励 $r_{forbid}=-1$
• 若行动达到目的地，奖励 $r_{target}=1$
• 其余行动，奖励 $r=0$

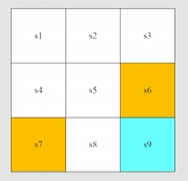
结果：在不同状态下用确定性的策略 $a_1,a_2,a_3,a_4,a_5$ 会有以下的奖励：

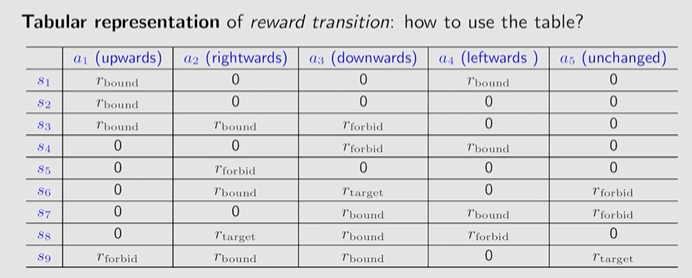
并且写成奖励的概率分布形式如下：$p(r=-1|s_1,a_1)=1$ and $p(r\ne -1|s_1,a_1)=0)$

• 从教育的角度看，如果付出努力了，就会得到正的收益，只是多少不确定
• 收益是取决于当前状态和做出的行动，与下一个状态无关。从教育角度看，只要付出努力了，都是值得鼓励的，尽管分数有高有低

Trajectory

Trajectory是一条状态-行动-奖励的轨道链，可一直持续下去

Trajectory 1: $s1\frac{a_2}{r=0}s2\frac{a_3}{r=0}s5\frac{a_3}{r=0}s8\frac{a_2}{r=1}s9$

Trajectory 2: $s1\frac{a_3}{r=0}s4\frac{a_3}{r=-1}s7\frac{a_2}{r=0}s8\frac{a_2}{r=+1}s9$

Return

Return 是一条 trajectory 的累计奖励，例如：

Trajectory 1 的 return 是 $return=0+0+0+1=1$

Trajectory 2 的 return 是 $return=0-1+0+1=0$

尽管都到达终点，但总体的 return 收益大，因此更好

Discounted return

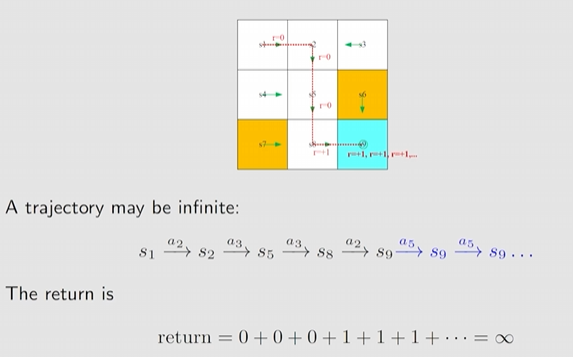
如果根据上述确定性的策略，这条轨道无限长且收益无穷大发散，因此需要引入 discount： $\gamma \in [0,1]$

discounted return = $0+\gamma 0+{\gamma }^{2}0+{\gamma }^{3}1+{\gamma }^{4}1+{\gamma }^{5}1+\dots ={\gamma }^3(1+\gamma +{\gamma }^2+\dots )={\gamma }^3\frac{1}{1-\gamma }$

Episode

• 在某决策下与环境的交互，智能体若停在某一个最终状态，这个时候的 trajectory 称作 episode，有限步的 trajectory 下的任务称作 episode tasks
• 若任务没有最终的状态，则这些任务称为 continue tasks
• Episode tasks 转换成 continue tasks，例如机器人寻路是有限的任务，但通过设置终点吸收态，让其下一步行动都是回到终点，

Markov decision process

• Set
  • 状态集 state：所有状态的集合 $S$
  • 行动集 action：所有行动的集合 $A(s)$ ，依赖于 $s$
  • 奖励集合 reward：所有奖励的集合 $R(s,a)$，依赖于 $s,a$
• 概率分布
  • 状态转移概率分布
    • $p(s^{\prime }|s,a)$，在当前状态 $s$ 和行动 $a$ 下，下一个状态 $s^{\prime }$ 的概率
  • 收益概率分布
    • $p(r|s,a)$ 在当前状态 $s$ 和行动 $a$ 下，收益为 $r$ 的概率
• 决策 policy
  • 在状态 $s$ 下，采取不同行动的概率 $\pi (a|s)$ 称为策略，这是行动的依据
• 马尔可夫性质：无记忆性，与历史无关
  • $p(s_{t+1}|a_{t+1},s_t,\dots ,a_1,s_0)=p(s_{t+1}|a_{t+1},s_t)$,
  • $p(r_{t+1}|a_{t+1},s_t,\dots ,a_1,s_0)=p(r_{t+1}|a_{t+1},s_t)$.
• 马尔可夫决策过程 markov decision process
  • Markov：无记忆性与历史无关
  • Decision：存在决策 policy
  • Process：状态根据行动到另一个状态
• 当 polily 给定后，即转移概率给定后，MDP 变为马尔可夫过程

Summury

• 状态
• 行动
• 状态转移、状态转移概率
• 奖励、奖励分布
• Trajectory、episode、return，discounted return
• 马尔可夫决策过程 MDP