课程笔记
Return
Return 的简单例子
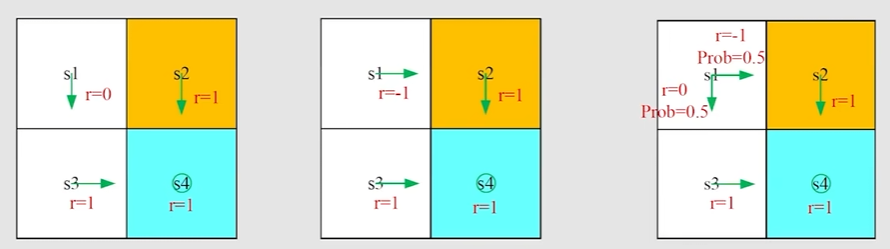
这三个相同环境下,给定三种策略,计算三种 return
return1=0+γ1+γ21+...=γ(1+γ+γ2+...)=1−γγ.
return2=−1+γ1+γ21+...=−1+γ(1+γ+γ2+...)=−1+1−γγ.
return3=0.5(−1+1−γγ)+0.5(1−γγ)=−0.5+1−γγ.
实际上 return 3 是两个 return 的平均,return 能够判断哪个 trajectory 是比较好的
return 一般计算方法
若每此行动都会得到相应的当步收益 ri,则 return 使用 boostrapping 方法计算(核心是状态之间是有关系的)
从 s1 出发 v1=r1+γr2+γ2r3+...=r1+γ(r2+γr3+...)=r1+γv2
从 s2 出发 v2=r2+γr3+γ2r4+...=r2+γ(r3+γr4+...)=r2+γv3
从 s3 出发 v3=r3+γr4+γ2r1+...=r3+γ(r4+γr1+...)=r3+γv4
从 s4 出发 v4=r4+γr1+γ2r2+...=r4+γ(r1+γr2+...)=r4+γv1
写成矩阵形式(矩阵形式很有用):
v1v2v3v4=r1r2r3r4+γ0001100001000010v1v2v3v4
有矩阵形式可化简为 bellman 公式 v=r+γPv ,通过方程求解 return v
State value
Definition
State value function 概念非常重要,是强化学习中策略的评估标准,以下逐步引出 state value 的公式表达
考虑单步过程: StAtRt+1,St+1
- t,t+1: 离散时间
- St: 在 t 时刻的状态
- At: 在 St 状态时采取的行动
- Rt+1: 采取 At 行动后获得的奖励
- St+1: 采取 At 行动后转移的状态
其中,大写字母 St,At,Rt+1 是随机变量,且单步过程中取决于概率分布:
- St→At 由策略 π(At=a∣St=s) 决定(采取行动又策略决定)
- St,At→Rt+1 由奖励概率 p(Rt+1=r∣St=s,At=a) 决定(获得奖励由奖励分布决定)
- St,At→St+1 由转移概率 p(St+1=s′∣St=s,At=a) 决定(状态转移由转移概率决定)
考虑多步轨迹 trajectory:StAtRt+1,St+1At+1Rt+2,St+2At+2Rt+3,...
Discount return 是 Gt=Rt+1+γRt+2+γ2Rt+3+...
- γ∈[0,1) 是折扣率。
- Gt 同样是一个随机变量,因为 Rt+1,Rt+2,... 是随机变量。
状态价值函数
其中 Gt 的期望被定义为 state-value-function
vπ=E(Gt∣St=s)
Remarks:
- 这是状态 s 的函数,是从状态 s 开始的条件下的条件 return 期望
- 该函数基于策略 π,不同策略 → 不同的轨迹 → 不同的 return → 会有不同的 state value
- 该函数表示状态 s 下的价值,价值函数越大,则该策略越好,因为能得到更多的累计奖励
- Return 和 state value 有什么区别?
- Return 是对单个 trajectory 计算的
- 而一般状态下,一个状态出发可能会有多个 trajectory ,求他们的期望 return
- 但如果策略是确定性的,那么 return 与 state value 是一致的
- 回到标题 Return 的简单例子,每种策略下只有一条 trajectory,因此 return 就是 state value,可以比较 state value 的大小来选择策略
State value 计算
State value 的计算工具:bellman 公式
从 return 一般计算方法 可知,bellman 公式描述了状态之间的联系
考虑 trajectory:StAtRt+1,St+1At+1Rt+2,St+2At+2Rt+3,...
则 return 利用 boostrap 化简:
Gt=Rt+1+γRt+2+γ2Rt+3+...=Rt+1+γ(Rt+1+γRt+3+...)=Rt+1+γGt+1
根据 state value 定义,利用上述技巧可化简:
vπ=E(Gt∣St=s)=E(Rt+1+γGt+1∣St=s)=E(Rt+1∣St=s)+γE(Gt+1∣St=s)
首先计算 state value 的第一项(实际上是 rewward的期望),使用两次全概率公式:
E[Rt+1∣St=s]=a∑π(a∣s)E[Rt+1∣St=s,At=a]=a∑π(a∣s)r∑p(r∣s,a)r
然后计算 state value 的第二项(实际上是未来 reward的期望),同样多次使用全概率公式
E[Gt+1∣St=s]=s′∑E[Gt+1∣St=s,St+1=s′]p(s′∣s)(t+1时刻有不同的状态转移)=s′∑E[Gt+1∣St+1=s′]p(s′∣s)(Markov的无记忆性)=s′∑vπ(s′)p(s′∣s)=s′∑vπ(s′)a∑p(s′∣s,a)π(a∣s)(s状态到s′状态有不同的行动)=a∑π(a∣s)s′∑p(s′∣s,a)vπ(s′)(写成未来state value的期望)
通过上述两项的计算,state value 计算式为:
vπ(s)=E(Rt+1∣St=s)+γE(Gt+1∣St=s)=a∑π(a∣s)r∑p(r∣s,a)r+γa∑π(a∣s)s′∑p(s′∣s,a)vπ(s′)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]∀s∈S
-
上述方程就是传说中的 Bellman 方程,描述了不同状态下的 state value函数的关系
-
该方程包含了两部分:当前 reward 的期望和未来 reward 的期望
-
对所有状态下都存在该等式关系
-
vπ(s) 和 vπ′(s) 是能够计算的 state value,但他们依赖于各种概率分布
-
给定策略 π(a∣s) 情况下,求方程解的过程被称为策略评估(方程解 vπ(s) 能评价策略的好坏)
-
奖励概率分布 p(r∣s,a) 和转移概率 p(s′∣s,a) 表示动态模型,一般是知道的(不知道也可以)
State value 计算例子
Example 1
给出如下环境、状态集合 S、确定性策略 π,其中行动分为上 (a1)、右 (a2)、下 (a3)、左 (a4)、不动 (a5)
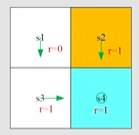
根据 Bellman 公式一般表达式,求解该环境下策略 π 的 state value 值 vπ(s)、vπ(s′),需要知道 π(a∣s)、p(r∣s,a)、p(s′∣s,a)
vπ(s)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]∀s∈S
首先考虑在 s1 状态下的 state value 值 vπ(s1)
- 策略 π(a=a3∣s)=1andπ(a=a3∣s)=0
- 奖励概率分布 p(r=0∣s,a)=1andp(r=0∣s,a)=0
- 状态转移概率 p(s=s3∣s1,a3)=1andp(s=s3∣s1,a3)=0
因此 s1 状态下 Bellman 公式化简为 vπ(s1)=0+vπ(s3),(本质上等于即时奖励+未来的 statevalue)
同理得到其他状态下的 Bellman 公式
vπ(s1)=0+γvπ(s3),vπ(s2)=1+γvπ(s4),vπ(s3)=1+γvπ(s4),vπ(s4)=1+γvπ(s4).
求解所有状态构成的 bellman 方程组,若 γ=0.9 则:
vπ(s1)vπ(s2)vπ(s3)vπ(s4)=1−γγ=1−0.90.9=9,=1−γ1=1−0.91=10,=1−γ1=1−0.91=10,=1−γ1=1−0.91=10.
可以观察到不同状态的 state value,s1 是最小的,因为离目标最远,而其他状态距离目标最近
Example 2
现在策略改变了,在 s1 处是随机方向。
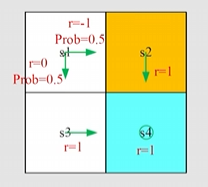
同上计算相似,,只在状态 s1 不同
vπ(s1)vπ(s2)vπ(s3)vπ(s4)=0.5[0+γvπ(s3)]+0.5[−1+γvπ(s2)]],=1+γvπ(s4),=1+γvπ(s4),=1+γvπ(s4).
同理解方程组:
vπ(s1)vπ(s2)vπ(s3)vπ(s4)=−0.5+1−γγ=1−0.90.9−0.5=8.5,=1−γ1=1−0.91=10,=1−γ1=1−0.91=10,=1−γ1=1−0.91=10.
比较 example 1 与 example 2 两种策略可知
在 s1 下,vπ1(s1)>vπ2(s1),显然第一种策略更好。
Bellman equation
Bellman 公式的矩阵形式
因为每一个状态都会存在一个 Bellman 公式,因此具有矩阵形式。,Bellman 公式如下:
vπ(s)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]∀s∈S
将 Bellman 公式使用符号简化,得到:
vπ(s)=rπ(s)+γs′∑pπ(s′∣s)vπ(s′)∀s∈S
其中
rπ(s)≜a∑π(a∣s)r∑p(r∣s,a)r,pπ(s′∣s)≜a∑π(a∣s)p(s′∣s,a)
因此若状态表示为 si(i=1,...,n),则对于状态 si 的 Bellman 方程为
vπ(si)=rπ(si)+γsj∑pπ(sj∣si)vπ(sj)
将所有状态的 Bellman 方程写在一起,并重写称矩阵形式如下:
vπ=rπ+γPπvπ
其中
- vπ=[vπ(s1),...,vπ(sn)]T∈Rn
- rπ=[rπ(s1),...,rπ(sn)]T∈Rn
- [Pπ]ij=pπ(sj∣si) ,则 Pπ∈Rn×n是转移概率矩阵
Bellman 公式的矩阵形式例子
Example 1
若环境中只有四个状态,则 Bellman 公式的一般矩阵形式如下:
vπ(s1)vπ(s2)vπ(s3)vπ(s4)=rπ(s1)rπ(s2)rπ(s3)rπ(s4)+γpπ(s1∣s1)pπ(s1∣s2)pπ(s1∣s3)pπ(s1∣s4)pπ(s2∣s1)pπ(s2∣s2)pπ(s2∣s3)pπ(s2∣s4)pπ(s3∣s1)pπ(s3∣s2)pπ(s3∣s3)pπ(s3∣s4)pπ(s4∣s1)pπ(s4∣s2)pπ(s4∣s3)pπ(s4∣s4)vπ(s1)vπ(s2)vπ(s3)vπ(s4).
Example 2
若四个状态的环境中,给出如下策略:
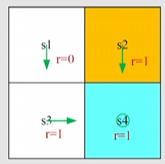
vπ(s1)vπ(s2)vπ(s3)vπ(s4)=0111+γ0000000010000111vπ(s1)vπ(s2)vπ(s3)vπ(s4).
Example 3
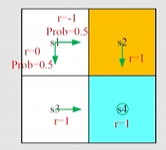
vπ(s1)vπ(s2)vπ(s3)vπ(s4)=0.5(0)+0.5(−1)0.5+1(−1)11+γ00000.50000.50000111vπ(s1)vπ(s2)vπ(s3)vπ(s4).
Bellman 公式的求解
解析解
vπvπ=rπ+γPπvπ=(I−γPπ)−1rπ
数值求解
迭代算法如下:
vk=rπ+γPπvk+1
算法中会产生一组序列 {v0,v1,v2,...},并有数值分析中的收敛结论:
vk→vπ=(I−γPπ)−1rπ,k→∞
相关数学证明过程

Action value
Definition
定义如下,表示在给定 state 和 action 下可以看出哪些 action 更好
qπ(s,a)=E[Gt∣St=s,At=a]
State value 与 action value 关系 1:从定义和全概率公式推 state value 具体表达
E[Gt∣St=s]vπ(s)=a∑E[Gt∣St=s,At=a]π(a∣s)=a∑π(a∣s)qπ(s,a)(action value的平均)
State value 与 action value 关系 2:从 Bellman 公式出发反推 action value 具体表达
vπ(s)qπ(s,a)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]=r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)
Action value 计算例子
Example
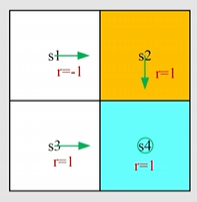
给定收益 p(r∣s,a)、转移概率 p(s′∣s,a) 则在 s1 处的
- 收益是 p(r=−1∣s1,a2)=1andp(r=−1∣s1,a2)=0
- 状态转移是 p(s=s2∣s1,a2)=1andp(s=s2∣s1,a2)=0
则由关系 2 计算在 s2 状态下的 action value
qπ(s1,a2)=−1+γvπ(s2)
虽然这里是确定性的策略,但不代表该策略是最优的策略,因此 qπ(s1,a1) 、qπ(s1,a3)、qπ(s1,a4)、qπ(s1,a5) 不一定为 0
qπ(s1,a1)qπ(s1,a3)qπ(s1,a4)qπ(s1,a5)=−1+γvπ(s1)=0+γvπ(s3)=−1+γvπ(s1)=0+γvπ(s1)
Summury
- State value vπ=E(Gt∣St=s)
- Action value qπ(s,a)=E[Gt∣St=s,At=a]
- Bellman equation (elementwise form)
- vπ(s)=∑aπ(a∣s)[∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vπ(s′)]∀s∈S
- Bellman equation (matrix-vector form)
- How to solve Bellman equation
- Closed-form solution
- Iterative solution






