代码部分
首先需要下载预备的工具包
install.packages("GDINA")
install.packages("ddpcr")
install.packages("effsize")生成 Q 矩阵
改错 Q 矩阵
源代码不区分 01 的错误顺序，都硬改，所以这个错误率不清楚是 0-1 还是 1-0 的比例 如果要分清楚的话不能使用源代码的随机生成，速度得不到保证，后续重复实验会很麻烦 应该
需要修改 python 中的 CDM 包
CDM 中实际上是计算了同一道题目在不同掌握模式下的回答概率
所以在源代码增加了两句，增加不同掌握模式的回答概率 = 掌握模式种类 * 题目数量
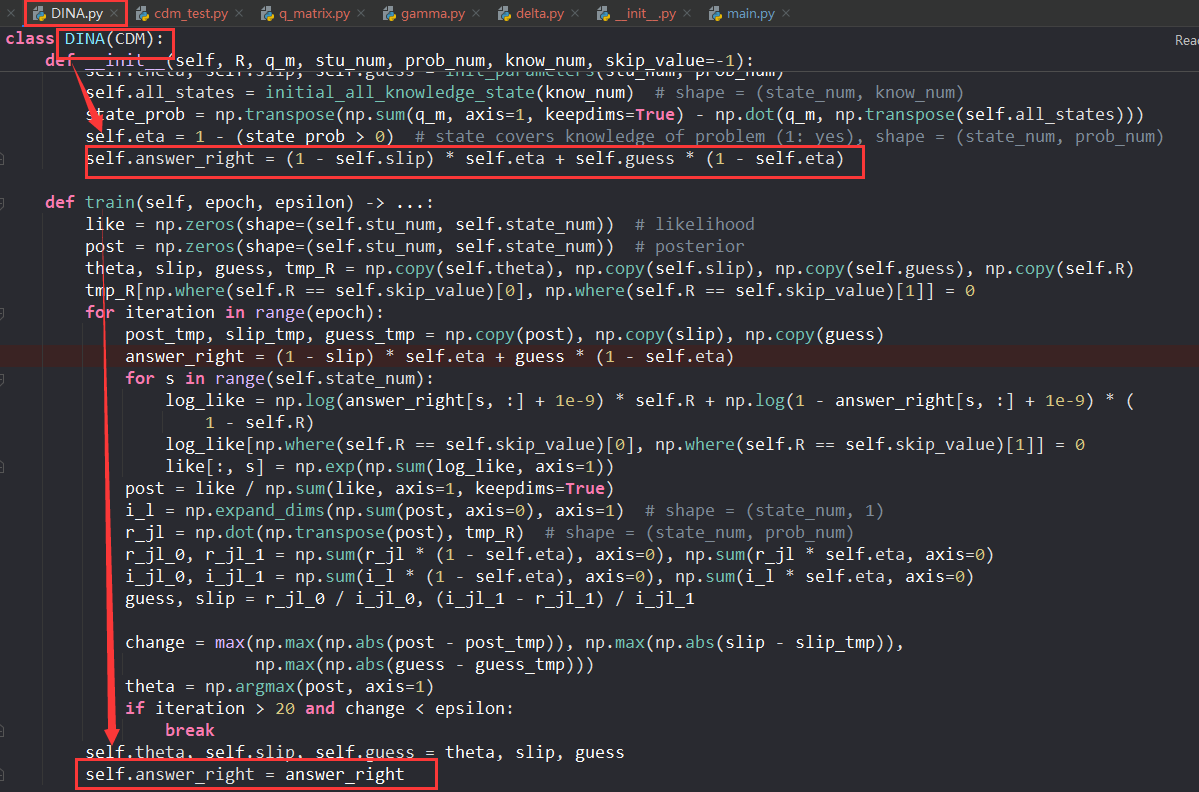
R 语言中的 GDINA 细节
孙代码中
sim.Q 生成Q
sim.WrongQ.rate 改错Q
sim.ORP.GDINA 生成一个模型下面数据格式是 sim. ORP. GDINA 函数生成，
32 道题目、
4 个知识点、
300 个学生、
16 种掌握模式
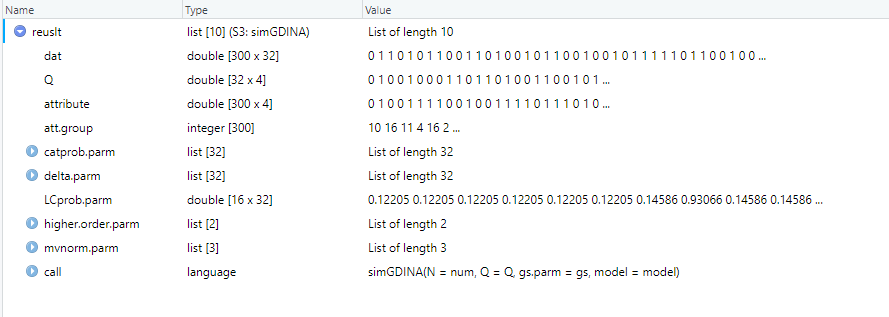其中 dat 是学生作答矩阵！
Q 是 Q 矩阵
attribute 三百个学生属于那种掌握模式
LCprob 是每道题目 (32)在不同掌握模式 (16)下的概率
问题是数据是怎么来的?？
结果是 GDINA 包自己按规则生成
上图种的dat数据来源是
dat=Y
而Y的来源是
att.Prob <- LC.Prob[att.group, ]
Y <- 1 * (att.Prob > matrix(runif(N * J), N, J))
知道学生的掌握模式att.group
查询学生对32道题目的回答正确概率 LC.Prob[att.group, ]
32道题目根据回答正确的概率生成01
"""
1.其中att.group是随机生成的idx
2.LC.Prob怎么来的:LC.Prob <- uP(as.matrix(par.loc), as.matrix(catprob.matrix))
1).其中par.loc是:par.loc <- eta(Q, pattern)
(1)eta函数
function (Q, AlphaPattern = NULL)
{
.Call("_GDINA_eta", PACKAGE = "GDINA", Q, AlphaPattern)
}
2).其中catprob.matrix是:catprob.matrix <- pd$itemprob.matrix
(1).pd <- gs2p(Q = Q, gs = gs.parm, model = model, no.bugs = no.bugs, type = gs.args$type, mono.constraint = gs.args$mono.constraint, digits = 8)
"""
或者
for (j in 1:S) {
Pj <- att.Prob[, which(C0 == j)]
Y[, j] <- apply(Pj, 1, function(x) {
sample(c(0:C[j]), 1, prob = x)
})
}delta 法 debug
在 delta 法中如果知识点数量只有 3，是有可能出现 q=[1,1,1]比两个知识点好，但仍然没有退出循环 4，的话就是可能出现 q=[1,1,1,1]比其他好，但仍还没有跳出循环，所以加上设定
gamma 法 debug
出现 es 为 0 的情况！全部加 1 e-6
Hypothesis 法 debug
在循环检验时，python 的 new 与 old 向量一定要注意 copy() 因为函数内部变量发生改变，函数外的变量也会发生改变！所以放进函数内的参数最好要 copy！ 例如
# 此处在函数里面对modify_q_m进行了修改，所以需要copy一份，保证不影响原来的q_modify_old
q_modify_old = self.q_m.copy()
q_modify_new = self.no_loop_modify_Q(modify_q_m=q_modify_old.copy(),**kwargs)generate data debug
Q 矩阵的错误设置需要有限制 但是作答矩阵错误设置不需要限制，所以应该直接改！
生成学生掌握真值
什么规则？
- 均匀抽样，这种中间的较多
- 正态抽样，怎么正态法，4 个知识点
- 用正态抽样意为：不同知识点[1,2,3,4]对应为等概率分位点[-0.84162123, -0.2533471 , 0.2533471 , 0.84162123]
- 生成独立多元正态随机数 100 × 4 表示 100 个学生的掌握模式
- 因为时正态分布的随机数，因此
理论部分
假设检验法
根据统计量与概率分布，得出拒绝或者接受的结论 当拒绝原假设时，即认为原本的 不正确，可推出 的包含集也不正确，说明该掌握模式答错相应题目数量很多，正确的 应该在非包含集 中。
若接受原假设，则无需修改，若拒绝原假设，则