认知诊断
输入 1:学生做题矩阵 , 表示第 个学生做第 道题目的对错
输入 2: 矩阵,,表示第 个道题目是否考察第 个知识点
认知诊断模型有很多,如简化的非补偿性认知诊断模型 、或者 、 等
以 为例,项目反应函数
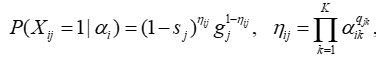 输出 1:预测学生对 个知识点是否掌握
输出 2:估计 类模型中的猜测参数 ,和失误参数
输出 1:预测学生对 个知识点是否掌握
输出 2:估计 类模型中的猜测参数 ,和失误参数
假设检验
符号定义
- 学生数量:
- 题目数量:
- 知识点数量:
- 作答矩阵:,其中 表示第 个学生对第 道题目的作答对错,正确为 1,错误为 0
- 矩阵:, 学生掌握情况矩阵
- 为第 题对 个知识点的考察情况,考察记为 1,未考察记为 0
- 为第 个学生对 个知识点的掌握情况,掌握记为 1,未掌握记为 0
- 表示 中的每个分量不小于 中的对应分量,即对 都有
- 表示 矩阵的子矩阵,特别的表示 矩阵的第 行
- 定义运算 , 表示 矩阵去除第 行 向量,记
- 同理 ,表示作答矩阵 去除第 列作答向量,记
- 借用集合中的定义: 表示 ,推到矩阵上的定义
思路
以第 道题目为例
- 第一步: 模型输入 ,输出第 题的猜测参数 ,失误参数 ,每个学生的掌握情况
- 第二步:设计方法推出某个 可能存在问题,并且能推出是属性缺失问题,还是属性冗余问题 (也可以直接遍历所有题目,不用判断是否缺失冗余)
- 第三步: 模型输入 ,输出 道题目的猜测参数 和失误参数 ,以及每个学生的掌握情况 。此步骤作用是为了降低第 题 向量错误导致其他参数估计的误差。
- 第四步:确定假设检验问题
- 情形一:判断出来是属性缺失问题
- 情形二:若判断出来是属性冗余问题
- 情形三:同时存在属性缺失和冗余问题,首先按.. 待推导
- 第五步:选择样本
- 若为情形一缺失情况
- 则建立假设:
- 选择满足以下规则的样本,输入某道题目的 向量,指定第 个知识点,以及
- 建立统计量:根据 中的学生,计算作答第 题的错误数量 ,
- 原假设成立时,样本 中的学生具有做对 考察模式题目的掌握模式,因此做第 题错误只能是失误,因此错误概率为 估计的失误参数。但 模型的输入为 ,输出无第 题的失误参数,因此采用其他题目的平均作为估计,,统计量服从二项分布:
- 原假设不成立时,,即第 题考察了第 个知识点,而 中的学生均未掌握第 个知识点,因此做错的数量会更多, 有偏大的趋势,拒绝域形式为 。即
- 给定置信度 进行检验:
- 【缺失属性例子 1】
- 真实 向量为 ,
- 当下错误 向量为
- 判断出第 题是缺失情况,则
- 根据 估计了除第 题外的 ,因此第 题的估计 ,估计了学生的掌握模式
- 若第 个知识点存在缺失属性的情况
- 根据错误的 筛选样本
- 筛选的掌握模式属于以下类型:
- 筛选的掌握模式属于以下类型:
- 计算统计量:样本 做第 题的错误数量 ,如果假设正确,则做错只可能是失误,,例如
- 则计算累计概率
- 因为错误题目太多了,拒绝原假设,则修改 矩阵为
- 【缺失和冗余同时存在的例子】
- 若为情形二冗余情况
- 则建立假设:
- 选择满足以下规则的样本
- 建立统计量:根据 中的学生,计算作答第 题的正确数量 ,
- 原假设成立时,样本 中的学生掌握模式 相比 少了第 个知识点,所以做第 题时一定答错,如果对了那么只可能是猜对!因此猜测概率为 估计的猜测参数。但 模型的输入为 ,输出无第 题的猜测参数,因此采用其他题目的平均作为估计,,统计量服从二项分布:
- 原假设不成立时,,即第 题未考察了第 个知识点,而 中的学生此时做第 题一定做对的, 有偏大的趋势,拒绝域形式为 。即
- 给定置信度 进行检验(做对的人太多说明这题没考这么多知识点)
- 若为情形一缺失情况
实验设计
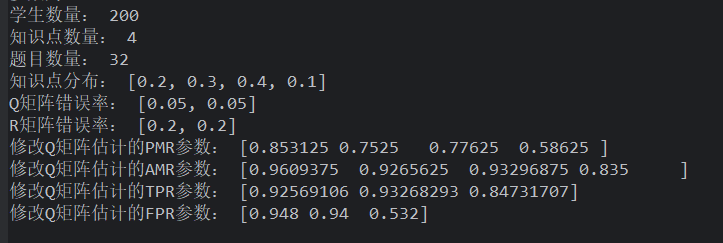
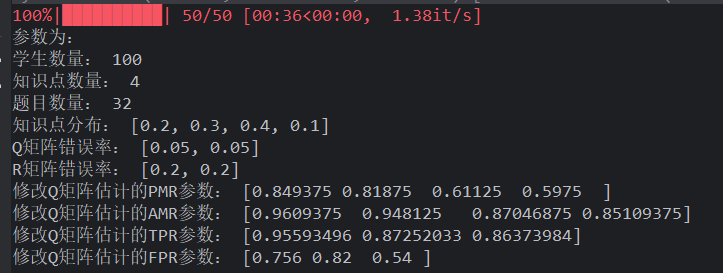
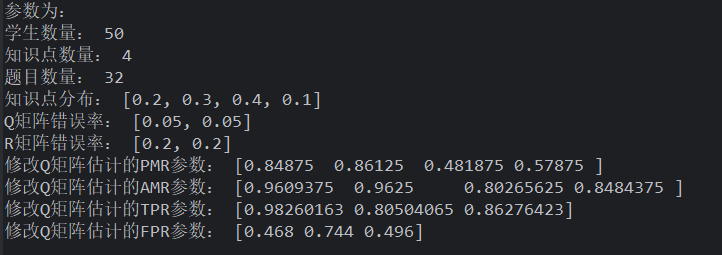
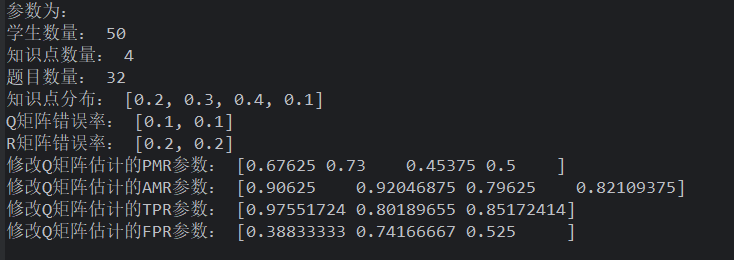
如果设置知识点数量为 4
正态分布的学生
可以看出:
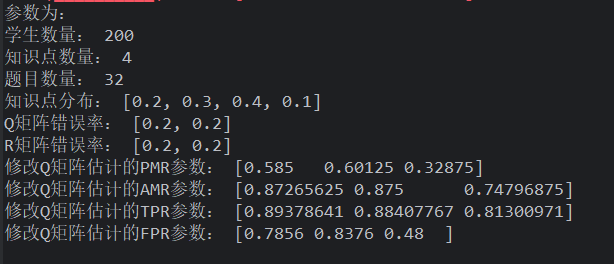
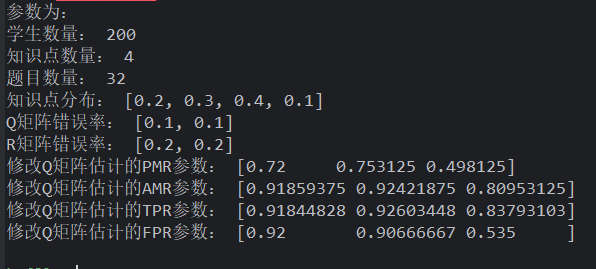
样本变少时,效果增强了

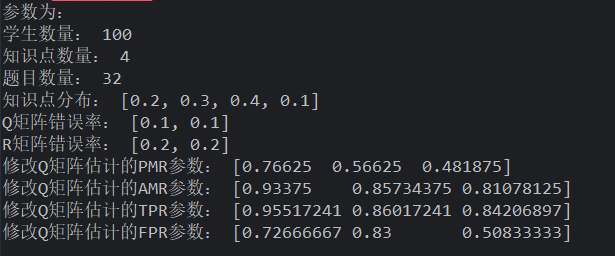
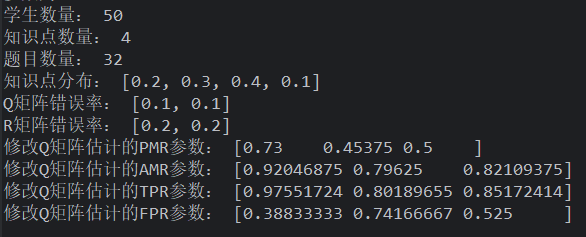
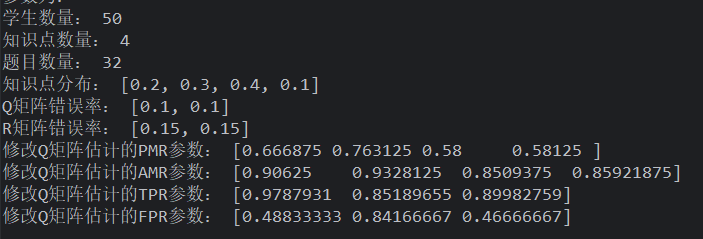
题目质量:质量越差,假设检验相对越好

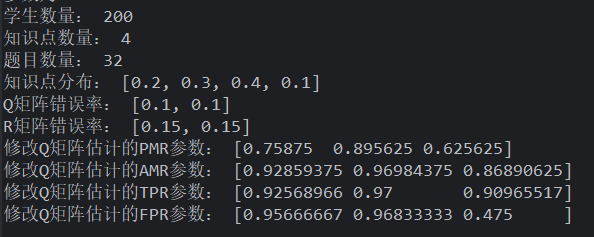
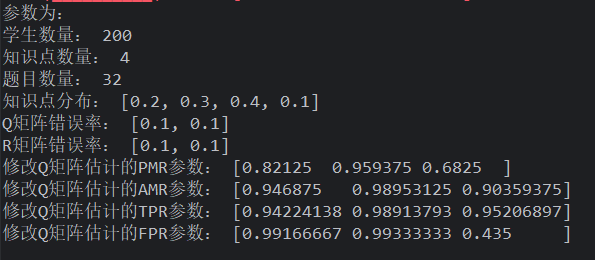
Q 矩阵错误率为 5%
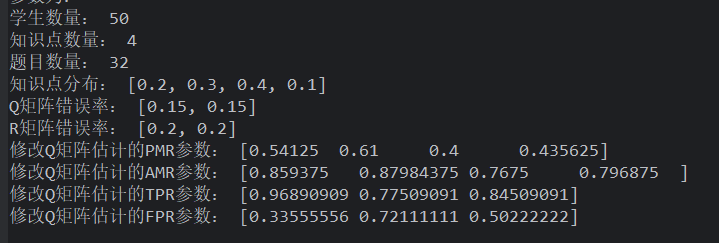
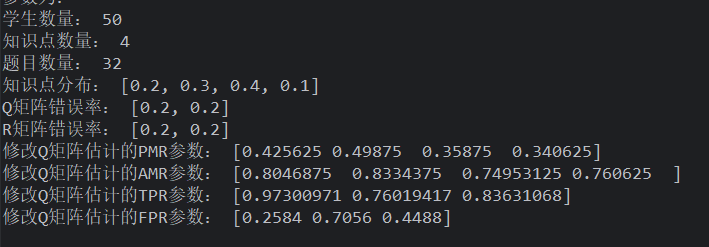
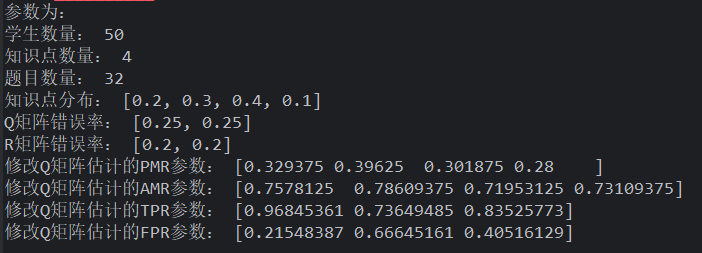
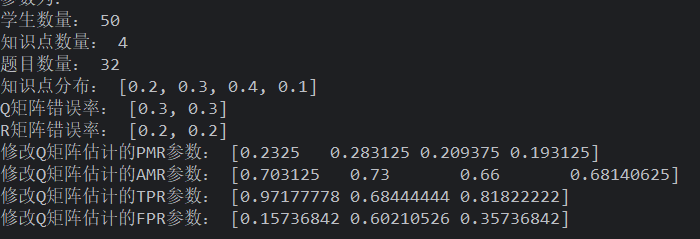
均匀分布的学生
均匀分布生成 Q 矩阵
均匀分布的 Q 矩阵和均匀分布的学生可能会有好结果 可能会让小样本的阈值稍微大点?
均匀 Q 矩阵和均匀学生下:题目数量
题目数量越多对假设检验越有利,因此构造样本时,应该要
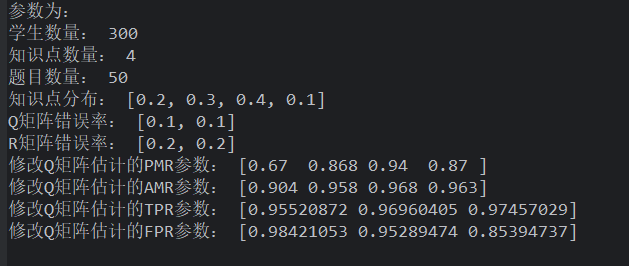
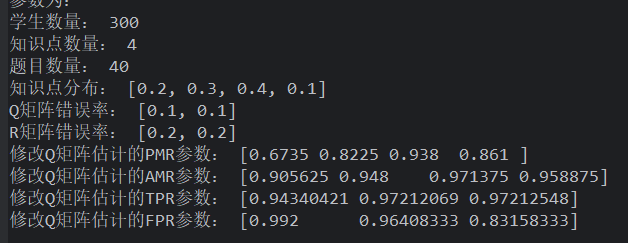

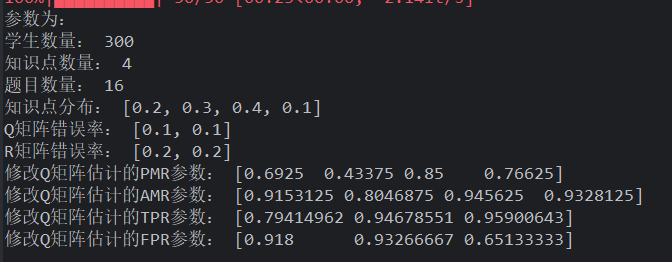 由上述知道题目数量越多越好,如果在题目为 50 的情况下,学生数量<200,开始有优势了
由上述知道题目数量越多越好,如果在题目为 50 的情况下,学生数量<200,开始有优势了
知识点变多能够把样本量阈值上提!
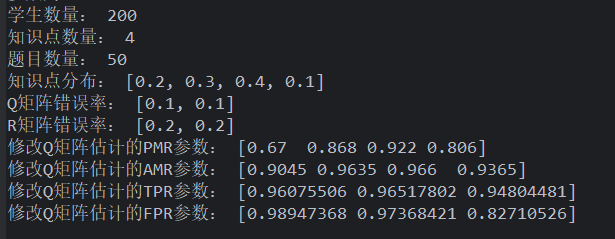
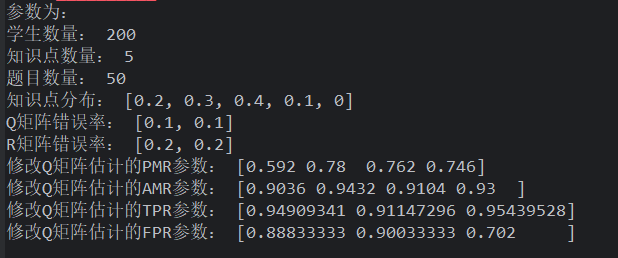
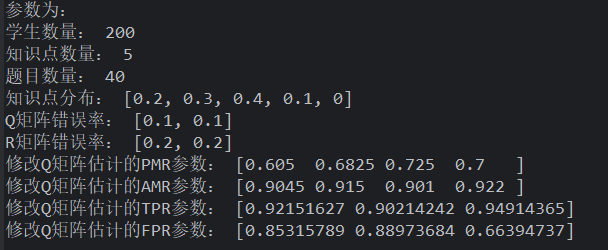
正态样本 mu=3,sigma=1, uniform Q 矩阵:正态学生样本能压住其他算法!
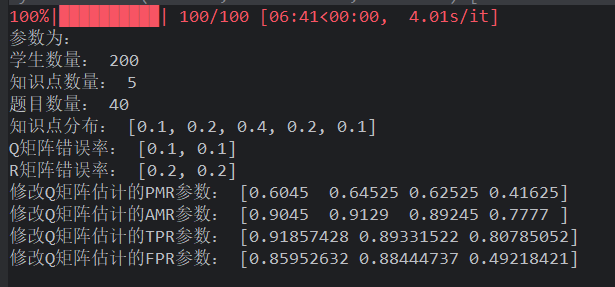
Uniform 样本,unifromQ 矩阵,
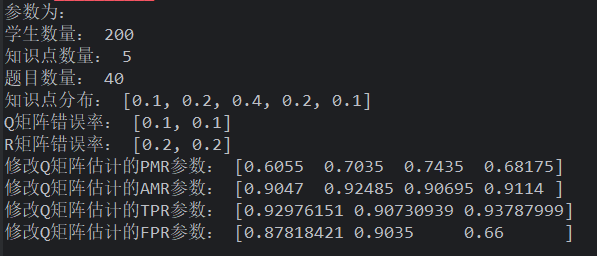
Uniform 样本,指定概率生成 Q 矩阵,指定概率 Q 生成压其他算法
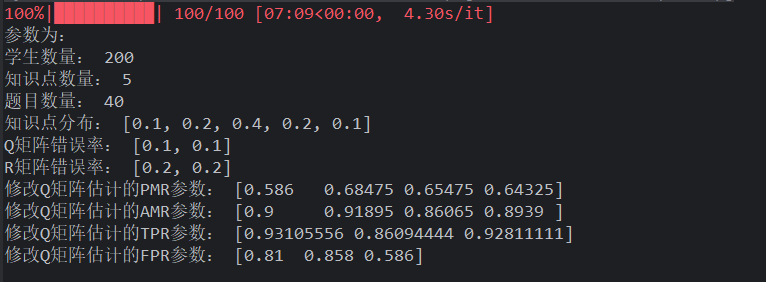
正态样本 mu=3, sigma=1,指定概率生成 Q 矩阵。连各种自定义生成样本,碾压!!
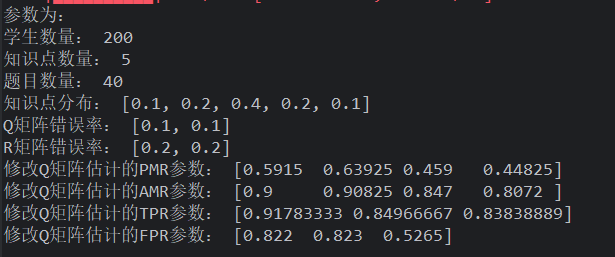
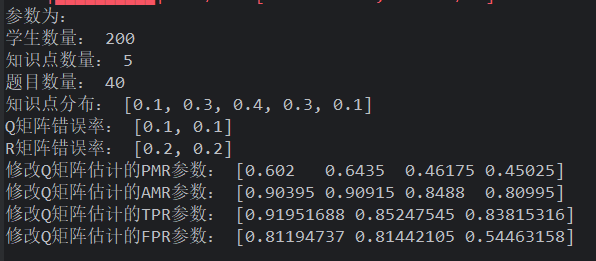 怎么样本变大了还更差了????
怎么样本变大了还更差了????
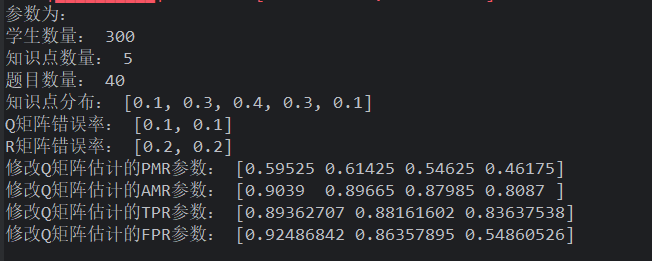
样本减小时才变得很强
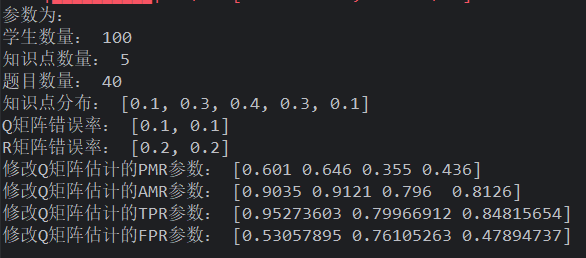
Q 矩阵错误率提高了,有利于修正回来幅度大
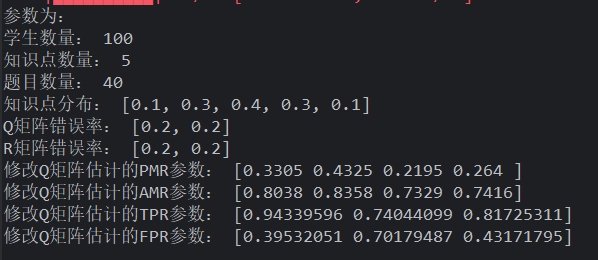
题目质量高一点,也有利于全部算法性能提升,但算法之间相对 delta 上升更快
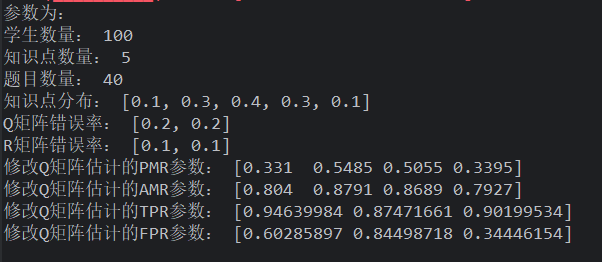
质量达到最高时,delta 法就是最高了 (在样本 100 的情况下)
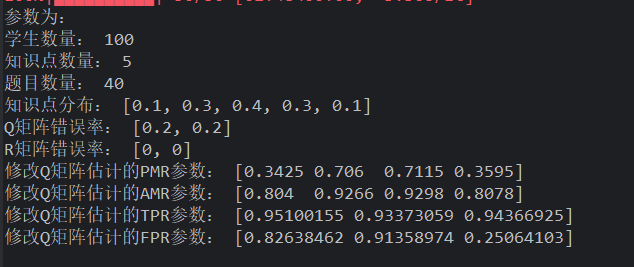
直接杀疯了
Q 矩阵和学生状态生成均按照知识点 states 中比例生成
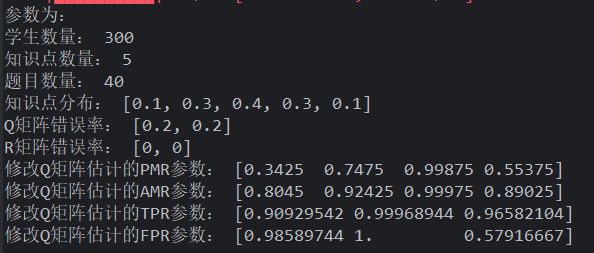
现在提高 R 错误率,题目质量降低,依旧比 gamma 法好!,但还是不如 delta 法
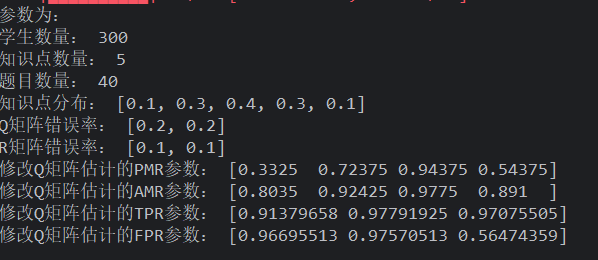
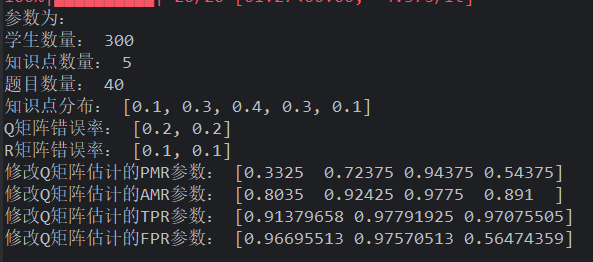
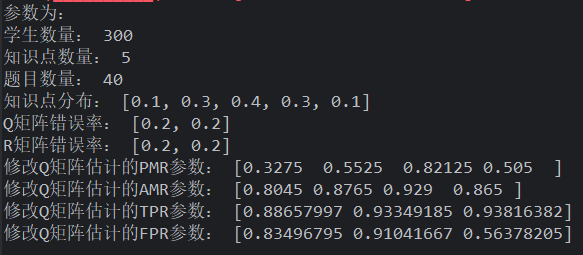
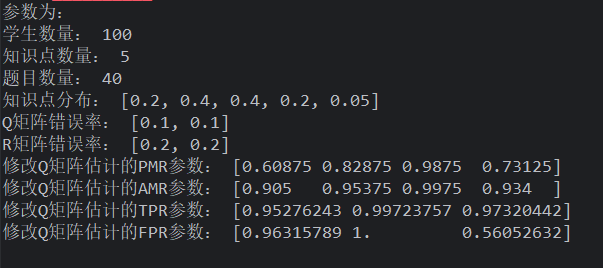
频率生成学生,uniform 生成 Q,R 用题目随机修改
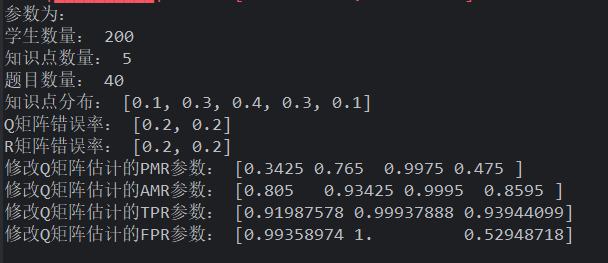
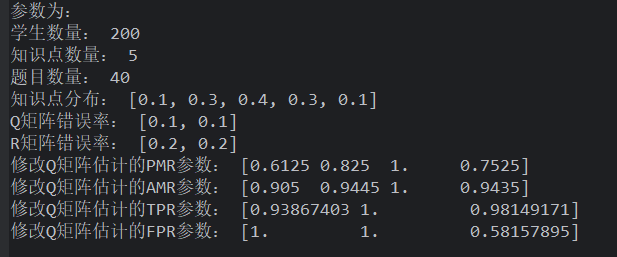
使用 normal 法生成学生,Q 矩阵频率生成,R 作答 gs 生成(Q 错误越多,越能超越 dalta 法)
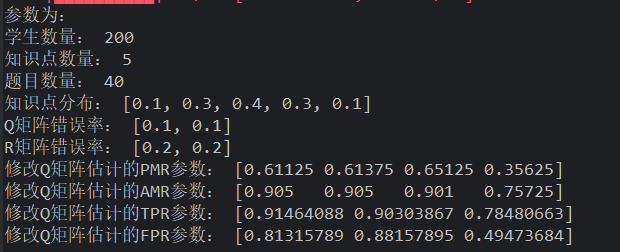
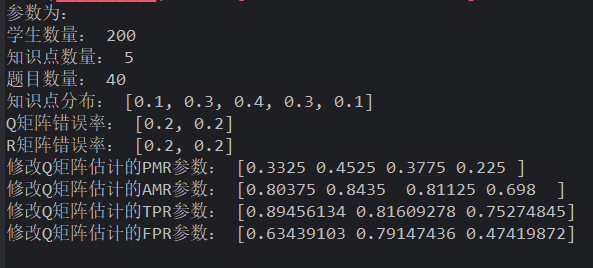
使用 prob 概率生成 Q,综合性题目较多的题目、使用正态分布生成学生,作答随机生成错误
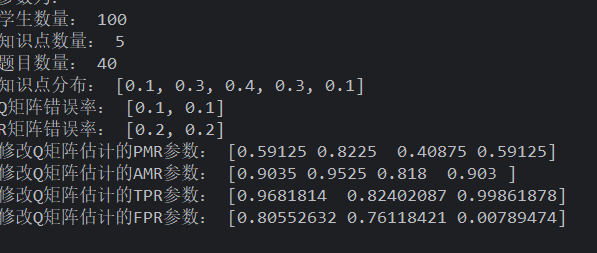
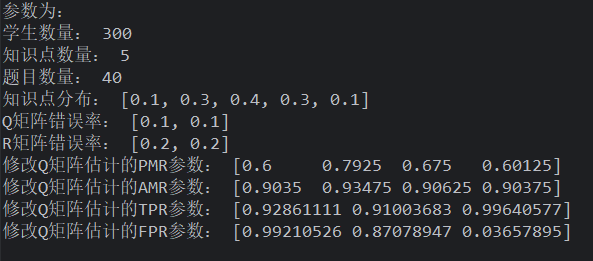
使用 prob 概率生成 Q,综合性题目较多的题目、使用正态分布生成学生,作答按 gs 生成
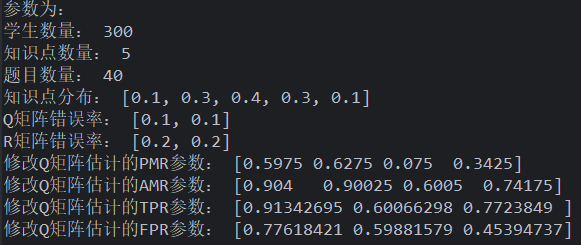
概率 Q+频率学生+gsR(不可取)
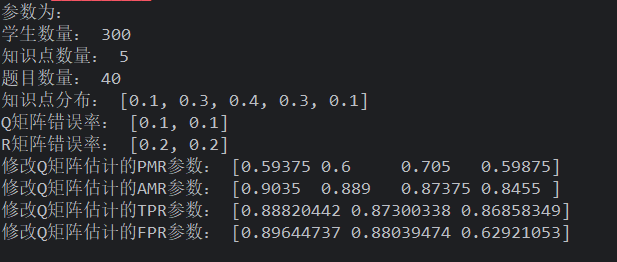
使用 frequency 生成学生和 Q,作答矩阵 R 用 gs 生成(完蛋) Q 矩阵错误越低,则普遍提升越高,而样本减少则,ht 效果提升了
不推荐拿这种方式比较
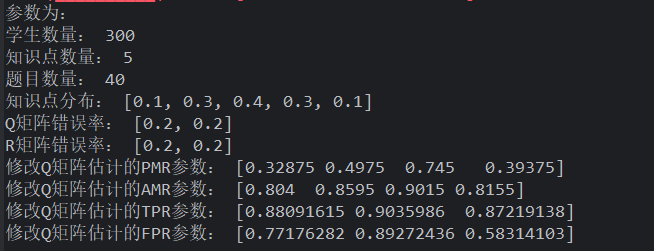
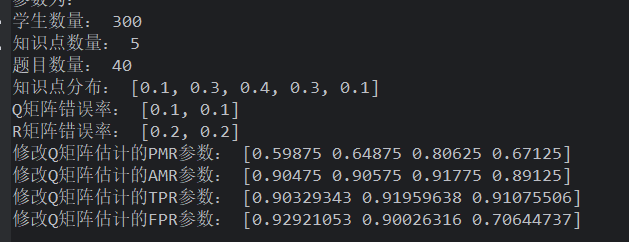
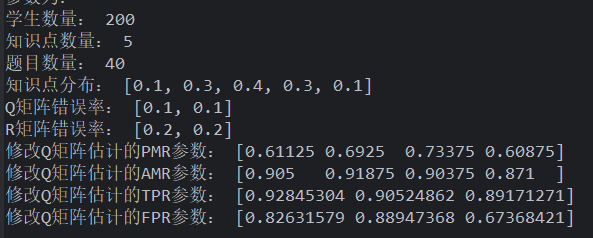
uniform 学生+指定 Q 错误率生成+**
指定概率生成 Q
uniform
frequency
正态学生 mu=2,sigma=1+指定 Q 错误率生成+***
指定概率生成 Q
sigma=1
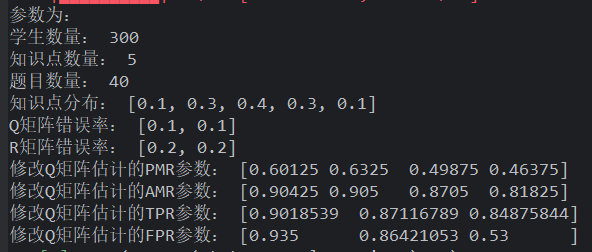 sigma=0.5
sigma=0.5
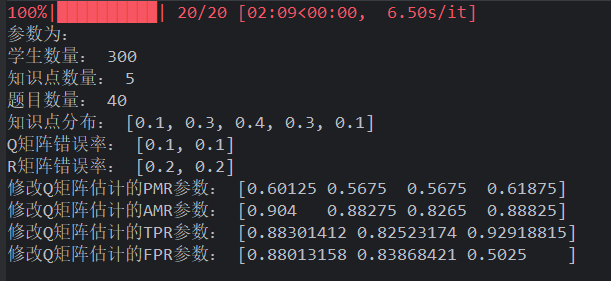 sigma=0.5,mu=3
sigma=0.5,mu=3
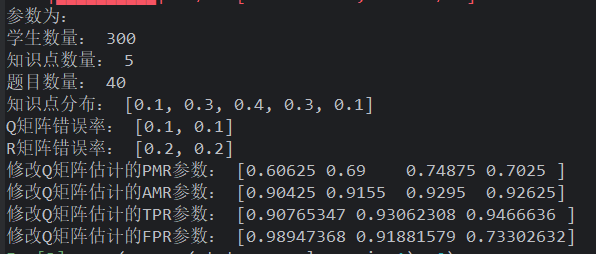 上图这完全是达不到普通要求,修改效率低!
上图这完全是达不到普通要求,修改效率低!
Uniform
Frequency
思考
分析
真实q=[1,0,0]
错误q=[1,1,0]
遍历第一个知识点是,发现[0,1,0]这帮人做对数量还挺多的,但没到拒绝域,不拒绝
遍历第2知识点,发现[1,0,0]这帮人做对很多,因此2知识点冗余,马上修改【保护qj2=1的原假设】
遍历第3知识点,发现[1,0,0]这帮人做错也多也拒绝【保护qj3=0的原假设】假设检验算法分析
试验变量 被试人数: 属性个数: 被试分布: 项目数量与属性个数比: 项目质量: Q 矩阵错误比例: 显著性水平
初步分析:
学生数量
假设检验谨慎保留,有足够把握才修改错误 q 向量。优势是学生数量越少越稳定,修正 Q 矩阵不容易把原来正确的修改。但是 dleta 法和 gamma 法在学生数量较少时,将大量的正确 Q 矩阵修改错误,导致原本错误的 Q 矩阵更错误
样本越大、导致错误修改率变高,但是正确被修改了也多,为了数据好看,需要提高 Q 矩阵错误率
- 所以样本越大,同时 Q 错误率越高,会越好
- 题目质量越差(学生答题误差越大),假设检验效果(相对)越好,即越稳定
- Q 矩阵错误越多,效果与不好!
- 这个和第一点似乎有冲突
- 在 QR 错误都很高的情况下,样本越大,相对越差!,样本越少,相对越好!
实验设计确定
- 自己内部控制的随机性
- Q 矩阵生成最好采用概率生成、其次是 uniform 均匀分布
- 学生矩阵生成采用特别的
- 超参数:
- Q 矩阵错误率(结论:错误越高,修正幅度越大!)
- 作答失误率【可看成题目质量】(结论:质量越高-失误率越低,则全部算法提升幅度都能提升)
- 置信度
- 知识点考察个数,越多对假设检验越好,因为样本相对的减少了!4.5
除了实验设计,还需要将 dealtorre 的 Q 矩阵保持一致
sg 参数均值均为 0.2 人数 5000 属性 5 项目 30 个
研究一:假设检验算法自己的参数选择特性
研究 1 数据存在问题! 在作答失误率为 5%时,当 Q 矩阵失误率提高,假设检验法同样能够将其修正,
- 特别是在 Q 矩阵失误率小于 20%的情况下,修正比例达到 100%
- 同样的,在作答失误率为10 %,Q 矩阵失误率小于 15%时,能够 100%修正
- 通过对比发现,作答失误率越高,修正的比例
结论一:作答失误率对准确率的影响,
- 从表 1、2、3、4 的结果中可看出,无论在何种作答失误率的情况下,假设检验法均能有效修正 Q_wrong,且修正后的准确率明显提高,且作答失误率越低,准确率越高。 结论二:置信度对准确率的影响
- 置信度在 0.01、0.05、0.1 时,假设检验法的修正性能几乎没有区别,表明该方法对超参数置信度的变化并不敏感,体现了算法中统计理论的稳定性,具有广泛适用性。
- 在设置置信水平分别为 0.01、0.05 以及0.1 的情况下,经过严谨的假设检验分析,我们可以观察到该方法的校正性能表现出高度的一致性,意味着该算法对于超参数置信度的选取具有优异的稳健性。这不仅验证了统计理论的可靠性,还提供了广泛的适应性。 结论三:Q 矩阵错误率对准确率影响
- 在 Q 矩阵错误率较低时(尤其在错误率小于 10%时,见表 1、2),假设检验法的属性准确率基本能达到 100%,表明该方法具有较强的识别能力。
分析表 1 至表 4 的数据可看出,无论在何种预设的作答失误率水平上,采用的假设检验法均能有效修正 Q_wrong,且修正后的准确率明显提高;除此之外,随着作答失误率降低,其判别能力越精确,准确率趋于立项的 100%;在设置置信水平分别为 0.01、0.05 以及 0.1 的情况下,经过严谨的假设检验分析,我们可以观察到该方法的校正性能表现出高度的一致性,意味着该算法对于超参数置信度的选取具有优异的稳健性。这不仅验证了统计理论的可靠性,还提供了广泛的适应性;在 Q 矩阵错误率较低时 (尤其在错误率小于 10%时,见表 1、2),假设检验法的属性准确率基本能达到 100%,表明该方法具有较强的识别能力。
研究二:假设检验与其他算法的性能理论性能比较
1.模式准确率与属性准确率的分析
分析样本量相关的结论,然后再时作答错误率=题目质量。讨论分为大样本情形与小样本情形,
- 在样本量较小的情形下
- 首先,若作答错误率还进一步提升, 法与 法会产生”反向”修正情况,即修改的 Q 矩阵比错误的 Q 矩阵更多错误,可以理解为题目质量越差,现有算法越容易出现”欠拟合”情况。
- 这是因为样本量太少导致 es 、gs 估计严重有偏导致 法与 法修正无法准确发现正确的模式和属性,甚至出现误判,这是不可接受的。
- 其次,假设检验对模式和属性的修正性能稳定性和准确性要远高于其他算法。
- 这是因为假设检验中根据小概率事件原理,不轻易拒绝原假设,尽可能保证原有的正确的属性仍然维持正确。只有足够把握的情况下,才选择修正。因此相对与 法与 法而言,受样本量的影响较小。
- 首先,若作答错误率还进一步提升, 法与 法会产生”反向”修正情况,即修改的 Q 矩阵比错误的 Q 矩阵更多错误,可以理解为题目质量越差,现有算法越容易出现”欠拟合”情况。
- 在样本量较大的情形下,
- 首先, 法与 法”欠拟合”的情况会逐渐消失,其两种准确率会得到较大的提升。
- 其次,虽然假设检验法与其他算法之间的差异会变小,甚至在 Q 矩阵错误率为 20%时被 法超过的情况,但假设检验深厚的理论基础和广泛地适用性,为其始终较高的模式和属性准确率提供严谨地保障。
- 最后,三种算法对作答失误率不敏感,即在大样本情形下,题目质量不是影响修正效能的关键。
2 .正确属性保留率与错误属性修正率
Q 矩阵错误率一般较低是一个合理的假设,这意味着大多数属性是正确的,而错误的属性仅占少数。假设检验展现出显著的优势:它能极好地保留原本正确的属性,正如表6所示,其正确属性保持率名列前茅。尽管在修正错误属性方面,其表现可能并非总是最佳,但鉴于 Q 矩阵本身错误较少的特点,这种偏重于保护正确信息的方法使得其整体效能依然领先。
3.总结
总的来说,在统计理论基础的保证下,在样本数据少、题目质量低的情况时,相比于 法与 法,假设检验方法对 Q 矩阵修正的准确率有着得天独厚的领先优势
总的来说,假设检验方法在修正 Q 矩阵的准确率上展现出独特的优势,尤其在面临样本量有限且问题质量不高的情况下。这一优势建立在坚实的统计理论
总的来说,假设检验方法在修正 Q 矩阵的准确率方面展现出独特的优势,这一特性在处理样本量相对有限且数据质量问题较为突出的情形下显得尤为重要。假设检验法的核心不仅在于提供了系统性的框架判断观测结果是否纯粹由随机变异引起,更在于其能有效地减少由样本不足或项目噪声导致地误判风险。
将上述内容整合 :
在初步剖析了假设检验法的校正性能后,本研究深化探索,将其与 delta 法和 gamma 法进行对比分析,旨在全面评估假设检验法的可行性与准确性。
-
模式准确率和属性准确率 在样本量较小的情形下,首先,若作答错误率还进一步提升, 法与 法会产生”反向”修正情况,即修改的 Q 矩阵比错误的 Q 矩阵更多错误,可以理解为题目质量越差,现有算法越容易出现”欠拟合”情况。这是因为样本量太少导致 es 、gs 估计严重有偏导致 法与 法修正无法准确发现正确的模式和属性,甚至出现误判,这是不可接受的。其次,假设检验对模式和属性的修正性能稳定性和准确性要远高于其他算法。这是因为假设检验中根据小概率事件原理,不轻易拒绝原假设,尽可能保证原有的正确的属性仍然维持正确。只有足够把握的情况下,才选择修正。因此相对与 法与 法而言,受样本量的影响较小。 在样本量较大的情形下,首先, 法与 法”欠拟合”的情况会逐渐消失,其两种准确率会得到较大的提升。其次,虽然假设检验法与其他算法之间的差异会变小,甚至在 Q 矩阵错误率为 20%时被 法超过的情况,但假设检验深厚的理论基础和广泛地适用性,为其始终较高的模式和属性准确率提供严谨地保障。最后,三种算法对作答失误率不敏感,即在大样本情形下,题目质量不是影响修正效能的关键。
-
正确属性保留率和错误属性修正率 Q 矩阵错误率一般较低是一个合理的假设,这意味着大多数属性是正确的,而错误的属性仅占少数。假设检验展现出显著的优势:它能极好地保留原本正确的属性,正如表 6 所示,其正确属性保持率名列前茅。尽管在修正错误属性方面,其表现可能并非总是最佳,但鉴于 Q 矩阵本身错误较少的特点,这种偏重于保护正确信息的方法使得其整体效能依然领先。
-
总结 总的来说,假设检验方法在修正 Q 矩阵的准确率方面展现出独特的优势,这一特性在处理样本量相对有限且数据质量问题较为突出的情形下显得尤为重要。假设检验法的核心不仅在于提供了系统性的框架判断观测结果是否纯粹由随机变异引起,更在于其能有效地减少由样本不足或项目噪声导致地误判风险。
研究三:假设检验算法在实证数据中的研究
实证数据思路, 若大家效果持平,则逐题分析 否则需要拟合度较高才行! 现在能用的数据是 timss2007,现在正在测试不同搭配的可用情况
- 法使用边发现边修正的方法 (代码中是 inherit) and 假设检验采用置信度 0.01

- 这显然 delta 法是足够强的,尽量不用
- 法使用边发现边修正的方法 (代码中是 inherit) and 假设检验采用置信度 0.05
- 法使用边发现边修正的方法 (代码中是 inherit) and 假设检验采用置信度 0.1
- 法使用边发现边修正的方法 (代码中是 dependence) and 假设检验采用置信度 0.01
- 法使用边发现边修正的方法 (代码中是 dependence) and 假设检验采用置信度 0.05
- 这是最好的结果

- 这是最好的结果
- 法使用边发现边修正的方法 (代码中是 dependence) and 假设检验采用置信度 0.1
可修改的算法思路
因为 法是每一次修正后都进行一次 cdm 诊断! 我们也可以!但试过了,效果变差了!甚至会出现没有考察的知识点!
为了系统地验证假设检验方法在实证数据下的校正性能,并开展与其他算法的实证对比分析,本研究依托了两大具有代表性的数据集:一是Tatsuoka(1990)搜集的FraSub数据集,另一则是倍受认可的TIMSS 2007数据集。FraSub数据集涵盖了536名学生的测试表现,他们在涉及5个认知领域的15项分数减法任务中接受了评估,该数据此前已被Douglas(2004)、Tatsuoka(2002)及de la Torre(2008)等诸多学者深入测量与解析。另一方面,TIMSS 2007则针对奥地利698名四年级生,通过25题覆盖11个认知维度,且被 Lee, Park, & Taylan (2011), Park & Lee (2014), 以及Park, Xing, & Lee (2018)等多篇研究用于探索教育评估和认知诊断领域。本研究旨在提供一个较为全面深入的视角,来检验和比较假设检验方法的有效性和实用性。
于 Tatsuoka (1984)分数减法数据, 研究二运 用 4 种方法对专家标定的 Q 矩阵进行修正。该测验 包括 15 个项目, 考察 5 个属性, 一共有 536 名被试 的作答反应。初始 Q 矩阵如表 9 中的 0、1 所示。 此外, 通过原始 Q 矩阵和各方法修正后 Q 矩阵的相 对拟合指标和绝对拟合指标比较不同 Q 矩阵的模 型数据拟合度。其中, 相对拟合指标包括偏差 (-2LogLikelihood, -2LL)、赤池信息准则 (Akaike information criterion, AIC)和贝叶斯信息准则(Bayesian information criterion, BIC), 绝对拟合指标包括 M2 、 RMSEA 和标准均方根残差(standardized root mean square residual, SRMSR)统计量。 表 9~10 分别是各种方法对专家界定的 Q 矩阵 的修正情况和模型数据拟合结果。由表 9 可知: ORDP、R、RMSEA 和 HD 方法分别调整了 24、32、 5 和 1 个属性。ORDP 方法未调整第 1、3、5、8、 9 和 11 题。由表 10 可知, 只有 ORDP 方法修正后 的 Q 矩阵的相对拟合指标均优于原始 Q 矩阵的值。 所有方法修正后的绝对拟合指标均低于原始 Q 矩 阵的结果, 且 ORDP 方法的 M2 和 RMSEA 值最低。 这表明采用 ORDP 方法修正后的 Q 矩阵与模型的 拟合度更优。值得注意的是, 各方法提出的修正方 案应作为专家修正 Q 矩阵时的建议, 研究者不能完 全依赖数据分析, 而忽视对项目特征的分析。
结论
这部分怎么写?已知很多知识点为 5 的数据集都被吊着打,但是知识点上升道到11 个的时候,反而优于其他算法 这是因为假设检验在样本量相对较低时倾向于维持原假设
结论大赏!
- 无论在何种预设的作答失误率水平上,采用的假设检验法均能有效修正 Q,修正后的准确率明显提高;且随着作答失误率降低,其判别能力越精确,准确率趋于理想的 100%
- 算法对于超参数置信度的选取具有优异的稳健性
- 在 Q矩阵错误率较低时(尤其在错误率小于10%时,见表 1、表2),假设检验法的属性准确率基本能达到 100%
- 与国内外同类研究相比,假设检验法在小样本环境中展现出更高的稳健性和优越性能、尤其在面临高作答失误率时,其优势更为显著。在大样本环境中,作答失误率对修正效果的影响力显著降低,得益于统计理论支撑,假设检验法依然维持保持强劲的竞争力。
无论在何 种预设的作答失误率水平上,采用的假设检验法均能有效修正 Q,修正后的准确率明显提高,且随着作答失误率降低,其判别能力越精确,准确率趋于理想的 100%;在设置置信水平分别为 0.01、0.05 及 0.1 的情况下,经过严谨的假设检验分析,我们可以观察到该方法的校正性能表现出高度的一致性,意味着该算法对于超参数置信度的选取具有优异的稳健性,这不仅验证了统计理论的可靠性,亦展现了广泛的适应性;在 Q 矩阵错误率较低时,假设检验法的属性准确率基本能达到 100%,表明该方法具有较强的识别能力。 -================================ 改写成
- 假设检验法证明了其在各种作答错误率下的高效修正能力,显著提升 Q 矩阵准确率,且随错误率下降,其精确度逼近100%。
- 在不同置信水平下,该法展现了高度校正性能一致性,体现了对置信度选择的稳健性,进一步验证统计理论的可靠性及广泛适用性。
- 尤其在Q矩阵低错误率条件下,该法属性准确率近乎完美,彰显出卓越的识别效能。 总结三个点
- 假设检验法证明了各种作答错误率下的高效修正能力,显著提升 Q 矩阵准确率;在不同置信水平下,该方法具有非常稳定的性能,说明算法对于超参数的选取具有优异的稳健性;
- 与国内外同类研究相比,假设检验法在小样本环境中展现出更高的稳健性和优越性能、尤其在面临高作答失误率时,其优势更为显著。在大样本环境中,作答失误率对修正效果的影响力显著降低,得益于统计理论支撑,假设检验法依然维持保持强劲的竞争力。
- 在实证数据分析中,假设检验法不仅能增强认知诊断模型的拟合效能,而且在面对属性维度增多、样本量相对有限的复杂数据集时,相较于其他算法,其展现出更为显著的优势。
参考文献整理
引言的国家背景和时代背景 [1]教育部. 教育部2022年工作要点 [EB/OL].(2022-02-08)[2023-05-11]. http://www.moe.gov.cn/jyb_sjzl/moe_164/202202/t20220208_597666.html
[2]国务院关于深化教育改革全面提高义务教育质量的意见[EB/OL].(2019-6-23)[2019-7-8].https://www.gov.cn/zhengce/2019-07/08/content_5407361.htm.
[2]. 教育部等六部门关于推进教育新型基础设施建设构建高质量教育支撑体系的指导意见[J].中华人民共和国教育部公报,2021 (09): 15-19.
[3] 杨华利,耿晶,胡盛泽,等.人工智能时代的教育测评通用理论框架与实践进路[J].中国远程教育,2022(12):68-77.DOI:10.13541/j.cnki.chinade.2022.12.007.
[4]李昕蓉,王宇,肖佼,等.基于一流专业建设的教育测量学试卷评价分析及应用——以甘肃中医药大学为例[J].甘肃中医药大学学报,2024,41(01): 131-135.DOI: 10.16841/j.issn1003-8450.2024.01.25.
因而广受国际学术界及实践者的瞩目 [1] Huebner A , Wang C .A Note on Comparing Examinee Classification Methods for Cognitive Diagnosis Models[J]. Educational & Psychological Measurement, 2011, 71 (2): 407-419. DOI: 10.1177/0013164410388832. [1]DeCarlo, L. T .On the Analysis of Fraction Subtraction Data: The DINA Model, Classification, Latent Class Sizes, and the Q-Matrix[J]. Applied Psychological Measurement, 2011, 35 (1): 8-26. DOI: 10.1177/0146621610377081. [1] Torre D L ,J.DINA Model and Parameter Estimation: A Didactic[J]. Journal of Educational and Behavioral Statistics, 2009, 34 (1): 115-130. DOI: 10.3102/1076998607309474.
模型的实施框架涵盖了两大核心环节 gamma 法也要引用 [1]涂冬波, 蔡艳, 戴海琦. 基于 DINA 模型的 Q 矩阵修正方法[J]. 心理学报, 2012, 44 (4): 11. DOI: 10.3724/SP. J. 1041.2012.00558. [1] Tatsuoka K K .Cognitive Assessment: An Introduction to the Rule Space Method[M]. 2009.
矩阵的错误界定会对模型输出结果产生显著的消极影响 [1] Rupp A A .The Effects of Q-Matrix Misspecification on Parameter Estimates and Classification Accuracy in the DINA Model[J].Educational and Psychological Measurement,2008,68(1): 78-96.
delta 法 [1] Torre J D L .An Empirically Based Method of Q㎝atrix Validation for the DINA Model: Development and Applications[J]. Journal of Educational Measurement, 2008, 45 (4): 343-362. DOI: 10.1111/j.1745-3984.2008.00069.x.
法,不知道怎么叫 [1] Jimmy D L T , Chiu C Y .A General Method of Empirical Q-matrix Validation[J]. Psychometrika, 2016, 81 (2): 253-273. DOI: 10.1007/s 11336-015-9467-8.
D 2 方法 [1]喻晓锋, 罗照盛, 高椿雷, 等. 使用似然比 D^2 统计量的题目属性定义方法[J]. 心理学报, 2015, 47 (3): 10. DOI: 10.3724/SP. J. 1041.2015.00417. 残差方法 [1]Chen, Jinsong. A Residual-Based Approach to Validate Q-Matrix Specifications.[J]. Applied Psychological Measurement, 20 17:014662161668602. DOI: 10.1177/0146621616686021.
ICC 方法 [1]汪大勋, 高旭亮, 蔡艳, 等. 一种非参数化的 Q 矩阵估计方法: ICC-IR 方法开发[J]. 心理科学, 2018, 41 (2): 9. DOI: 10.16719/j.cnki. 1671-6981.20180233.
[1]汪大勋, 高旭亮, 蔡艳, 等. 一种广义的认知诊断 Q 矩阵修正新方法[J]. 心理科学, 2019, 42 (4): 9. DOI:CNKI:SUN: XLKX. 0.2019-04-031.
RSS 方法 Chiu, C. Y. (2013). Statistical refinement of the Q-matrix in cognitive diagnosis. 海明距离法 [1]汪大勋, 高旭亮, 韩雨婷, 等. 一种简单有效的 Q 矩阵估计方法开发: 基于非参数化方法视角[J]. 心理科学, 2018, 41 (1): 9. DOI: 10.16719/j.cnki. 1671-6981.20180127.
相关研究文献(如Rupp & Templin, 2008; de la Torre, 2008)【】 [1] 鲁普 A A ,坦普林 J .DINA 模型 Q 矩阵错误规范对参数估计和分类精度的影响[J]. 教育与心理测量, 2008, 68(1):78-96. DOI:10.1177/0013164407301545.
[1] Leighton J P , Gierl M J , Hunka S M .The Attribute Hierarchy Method for Cognitive Assessment: A Variation on Tatsuoka’s Rule-Space Approach[J]. Journal of Educational Measurement, 2004, 41 (3): 205-237. DOI: 10.1111/j.1745-3984.2004. Tb 01163.x.
Nájera(2021) Nájera Álvarez P, Sorrel M A, de la Torre J, et al. Balancing fit and parsimony to improve Q-matrix validation[J]. British Journal of Mathematical and Statistical Psychology. 2021.
分数减法数据 [1] Tatsuoka K K .Toward an integration of item response theory and cognitive error diagnosis[J]. Diagnostic Monitoring of Skill and Knowledge Acquisition, 1990. 453-488
分数减法数据使用者 [1] Rupp A A , Templin J .The Effects of Q-Matrix Misspecification on Parameter Estimates and Classification Accuracy in the DINA Model[J]. Educational and Psychological Measurement, 2008, 68 (1): 78-96. DOI: 10.1177/0013164407301545. [1] Tatsuoka K K E .Analysis of Errors in Fraction Addition and Subtraction Problems. Final Report[J]. Kikumi K. Tatsuoka, 252 ERL, 103 S. Mathews St. Univ. Of Illinois, Urbana, IL 61801. 1984.
[1]DeCarlo, L. T .On the Analysis of Fraction Subtraction Data: The DINA Model, Classification, Latent Class Sizes, and the Q-Matrix[J]. Applied Psychological Measurement, 2011, 35 (1): 8-26. DOI: 10.1177/0146621610377081.
timss 2007 使用者 [1] Xiaoqing W , Shuliang D , Fen L .Q matrix and its Applications in Cognitive Diagnosis[J]. Journal of Psychological ence, 2019. [1] Lee Y S , Park Y S , Taylan D .A Cognitive Diagnostic Modeling of Attribute Mastery in Massachusetts, Minnesota, and the U.S. National Sample Using the TIMSS 2007[J]. International Journal of Testing[2024-05-29]. DOI: 10.1080/15305058.2010.534571. [1] Soo P Y , Young-Sun L , Kuan X .Investigating the Impact of Item Parameter Drift for Item Response Theory Models with Mixture Distributions[J]. Frontiers in Psychology, 2016, 7:255-. DOI: 10.3389/fpsyg. 2016.00255.
拟合指标体系 [1] Chen J , Jimmy D L T , Zhang Z .Relative and Absolute Fit Evaluation in Cognitive Diagnosis Modeling[J]. Journal of Educational Measurement, 2013, 50 (2): 123-140. DOI: 10.1111/j.1745-3984.2012.00185.x. [1]Liu Y ,Tian W ,Xin T .An Application of M 2 Statistic to Evaluate the Fit of Cognitive Diagnostic Models:[J]. Journal of Educational and Behavioral Statistics,2016,41 (1): 3-26. [1]Pablo N ,A M S ,Jimmy T L D , et al.Balancing fit and parsimony to improve Q-matrix validation.[J].The British journal of mathematical and statistical psychology,2020,74(S1): 110-130.