认知诊断
输入 1:学生做题矩阵 , 表示第 个学生做第 道题目的对错
输入 2: 矩阵,,表示第 个道题目是否考察第 个知识点
认知诊断模型有很多,如简化的非补偿性认知诊断模型 、或者 、 等
以 为例,项目反应函数
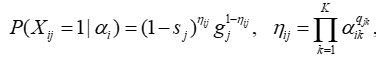 输出 1:预测学生对 个知识点是否掌握
输出 2:估计 类模型中的猜测参数 ,和失误参数
输出 1:预测学生对 个知识点是否掌握
输出 2:估计 类模型中的猜测参数 ,和失误参数
Q 矩阵理论
研究内容
矩阵是是认知诊断模型的基础,且 矩阵的精确性对模型的结果影响很大 但实际应用中 矩阵工作需要专家完成,且存在主观判断问题, 为了后续应用的准确性,需要对 Q 矩阵估计和修正
矩阵的性质
- 错误类型
- 属性冗余:题目没考某个知识点,但 Q 矩阵标记考了
- 属性缺失:题目考了知识点,Q 矩阵标记没考
- 属性冗余且缺失:同时存在
- Q 错误类型对模型影响
- 属性冗余:导致猜测参数 增大
- 属性缺失:导致失误参数 增大
- 结论: 越小, 矩阵越正确
修改 Q 矩阵相关工作
- 参数化方法
- 法(de la Torre):以修改一道题目向量为例
- 输入: 矩阵、学生作答矩阵
- step 1:将掌握 个知识点所有可能的 向量进行遍历替换
- step 2:将替换后的 Q 矩阵进行 DINA 模型诊断
- step 3:将掌握 个知识点的所有可能 向量遍历替换
- step 4:替换后的 Q 矩阵进 DINA 模型诊断
- step 5:若 ,说明 增大了,则
- 循环 step1-step 5,否则该题 矩阵修改为
- 法 (涂东波):以修改 道题中的 个知识点 为例
- 输入: 矩阵、学生作答矩阵
- step 1:对 进行 DINA 模型诊断估计一道题目的 ,估计学生知识点 掌握情况
- step 2:对是否掌握 分为掌握组和非掌握组
- step 3:计算效应大小, 为掌握组和非掌握组的作答标准差,
- step 4:修改准则
- 若 ,则
- 解释: 过大,说明 题 向量可能冗余,如果掌握和没掌握 知识点的人差别很小,
- 说明题目没考 知识点,因此确定为冗余。
- 若 ,则
- 解释: 过大,说明 题 向量可能缺失属性,如果掌握和没掌握 知识点的人差别很大,
- 说明题目 考了 知识点, 真缺失了第 个知识点
- 若 ,则
- S 统计量方法 (Liu)
- R 方法 (Yu)..
- 极大似然估计
- 法(de la Torre):以修改一道题目向量为例
- 非参数方法
- 欧氏距离法、海明距离法、曼哈顿距离法等
假设检验(孙)
包含集和非包含集概念
以项目考核模式为(1,1,0)为例
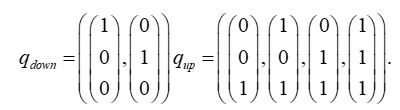 我们来看,若 存在冗余属性
则其包含集合为
我们来看,若 存在冗余属性
则其包含集合为
检验 Q 向量是否存在缺失属性
-
参数估计
- 根据已知 矩阵、作答矩阵 和 模型,
-
估计第 道题目的猜测参数 和失误参数
-
估计学生掌握模式:估计所有学生掌握模式
-
- 根据已知 矩阵、作答矩阵 和 模型,
-
建立假设(以第 道题目的 向量为例)
-
构造统计量
- 筛选学生掌握模式:筛选 向量这种掌握模式的学生
- (很可能找不到!找不到假设检验直接认为该 没错)
- 对这些掌握模式学生样本构造统计量:作答错误的学生数量 $$ X=n-\Sigma_{i \in S’}I(第k题是否做对),\quad n为q^k掌握模式的学生数量
- 筛选学生掌握模式:筛选 向量这种掌握模式的学生
- 给定显著性水平 下$$ P_{H_0}(X>r)=\alpha,\quad r=b_{\alpha}为二项分布的\alpha 上侧分位点
- 确定拒绝域
- 当 成立时,即真实 向量并非 这种冗余情况,则 DINA 估计猜测参数 比较正确。则在 这种错误掌握模式下的统计量服从二项分布:
- 当 不成立时,即真实 是属性更少的 ,如果按照这个掌握模式筛选学生,大多数都做第 题都做对,则 有偏大的趋势,拒绝域为 ,即 $$ W = {(x_1,x_2,…,x_n):Y > c}
拒绝原假设,存在缺失属性(不确定是否存在冗余属性)
-
取 的非包含集
-
建立假设 (同样为第 道题目的 向量)
-
构造统计量(同上)
- 筛选具有 这种掌握模式的学生 ,计算作答正确的学生数量 $Z$$$ Z=\Sigma_{S’}I(第k题是否做对)
- 确定拒绝域
- 当 成立时,真实的 向量是 这种冗余的情况,则失误参数估计 偏大
- 当 成立时,真实的 向量是 ,说明无缺失的情况,则猜测参数 估计比较正确
- 当 不成立时,真实的 并无缺失,这种掌握模式
假设检验
符号定义
- 学生数量:
- 题目数量:
- 知识点数量:
- 作答矩阵:,其中 表示第 个学生对第 道题目的作答对错,正确为 1,错误为 0
- 矩阵:, 学生掌握情况矩阵
- 为第 题对 个知识点的考察情况,考察记为 1,未考察记为 0
- 为第 个学生对 个知识点的掌握情况,掌握记为 1,未掌握记为 0
- 表示 中的每个分量不小于 中的对应分量,即对 都有
- 表示 矩阵的子矩阵,特别的表示 矩阵的第 行
- 定义运算 , 表示 矩阵去除第 行 向量,记
- 同理 ,,表示作答矩阵 去除第 列作答向量,记
- 借用集合中的定义: 表示 ,推到矩阵上的定义
思路
以第 道题目为例
- 第一步: 模型输入 ,输出第 题的猜测参数 ,失误参数 ,每个学生的掌握情况
- 第二步:设计方法推出某个 可能存在问题,并且能推出是属性缺失问题,还是属性冗余问题 (也可以直接遍历所有题目,不用判断是否缺失冗余)
- 第三步: 模型输入 ,输出 道题目的猜测参数 和失误参数 ,以及每个学生的掌握情况 。此步骤作用是为了降低第 题 向量错误导致其他参数估计的误差。
- 第四步:确定假设检验问题
- 情形一:判断出来是属性缺失问题
- 情形二:若判断出来是属性冗余问题
- 情形三:同时存在属性缺失和冗余问题,首先按..待推导
- 第五步:选择样本
-
若为情形一缺失情况
-
则建立假设:
-
选择满足以下规则的样本,输入某道题目的 向量,指定第 个知识点,以及
-
建立统计量:根据 中的学生,计算作答第 题的错误数量 ,
-
原假设成立时,样本 中的学生具有做对 考察模式题目的掌握模式,因此做第 题错误只能是失误,因此错误概率为 估计的失误参数。但 模型的输入为 ,输出无第 题的失误参数,因此采用其他题目的平均作为估计,,统计量服从二项分布:
-
原假设不成立时,,即第 题考察了第 个知识点,而 中的学生均未掌握第 个知识点,因此做错的数量会更多, 有偏大的趋势,拒绝域形式为 。即
-
给定置信度 进行检验:
-
【缺失属性例子 1】
- 真实 向量为 ,
- 当下错误 向量为
- 判断出第 题是缺失情况,则
- 根据 估计了除第 题外的 ,因此第 题的估计 ,估计了学生的掌握模式
- 若第 个知识点存在缺失属性的情况
- 根据错误的 筛选样本
- 筛选的掌握模式属于以下类型:
- 筛选的掌握模式属于以下类型:
- 计算统计量:样本 做第 题的错误数量 ,如果假设正确,则做错只可能是失误,,例如
- 则计算累计概率
- 因为错误题目太多了,拒绝原假设,则修改 矩阵为
-
【缺失和冗余同时存在的例子】
-
-
若为情形二冗余情况
-
则建立假设:
-
选择满足以下规则的样本
-
建立统计量:根据 中的学生,计算作答第 题的正确数量 ,
-
原假设成立时,样本 中的学生掌握模式 相比 少了第 个知识点,所以做第 题时一定答错,如果对了那么只可能是猜对!因此猜测概率为 估计的猜测参数。但 模型的输入为 ,输出无第 题的猜测参数,因此采用其他题目的平均作为估计,,统计量服从二项分布:
-
原假设不成立时,,即第 题未考察了第 个知识点,而 中的学生此时做第 题一定做对的, 有偏大的趋势,拒绝域形式为 。即
-
给定置信度 进行检验(做对的人太多说明这题没考这么多知识点)
-
-
思考
问题 1
问题 1:假设检验原假设不能写成 ,否则当 不成立,有两种情形
- Q 矩阵错误类型,属性缺失:
- 第 题的真实 在 中,即真实的 向量应该有更多属性,那么以当前少属性的 向量这种掌握模式的人去做第 题,显然错误比较多,所以统计量应该变大
- Q 矩阵错误类型,属性冗余:
- 第 题的真实 在 中,即真实的 向量应该有更少的属性,那么当前更多属性的 向量这种掌握模式的人去做第 题,正确率和前者相比正确率并没有太大变化。 因此第二种情形的 向量几乎没法拒绝,所以需要分情况讨论。
问题 2
题目质量太差的时候(一般不如 法) 题目质量不好导致学生猜对太多, 偏大,会导致二项分布 右偏,拒绝域右移,更难拒绝 就算 q 向量是错的,这个 q 向量的掌握模式也做对了很多题目,导致错误题目不足够多,没有把握认为 q 向量是错的。
问题 3
gs 的估计准确率对假设检验的影响是存在的,需要找到那些改不出来的题目查看原因
问题 4
对比 法是根据每道题目的 的大小判断所有向量的好坏
法是根据每道题目的 判断 q 向量缺失的属性,根据 判断 向量冗余的属性
假设检验法是根据每道题的考察知识点掌握的人做错的是否足够多,判断 q 向量是否缺失属性 根据每道题目考察知识点掌握的人做对的是否足够多,决定 q 向量缺失的属性 根据每道题目考察知识点掌握的人做对的是否足够多,决定 q 向量冗余的属性